\[{\Large{\text{Подобие треугольников}}}\]
Определения
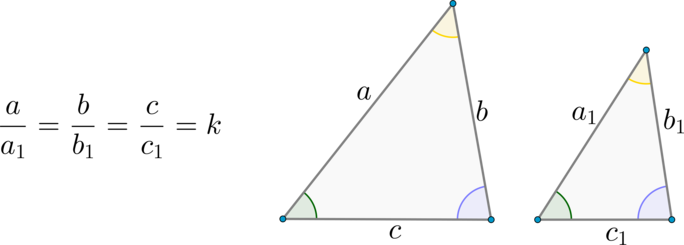
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).
Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.
Определение
Периметр треугольника – это сумма длин всех его сторон.
Теорема
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
Доказательство
Рассмотрим треугольники \(ABC\) и \(A_1B_1C_1\) со сторонами \(a,b,c\) и \(a_1, b_1, c_1\) соответственно (см. рисунок выше).
Тогда \(P_{ABC}=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=k\cdot
P_{A_1B_1C_1}\)
Теорема
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Доказательство
Пусть треугольники \(ABC\) и \(A_1B_1C_1\) подобны, причём \(\dfrac{AB}{A_1B_1} = \dfrac{AC}{A_1C_1} = \dfrac{BC}{B_1C_1} = k\). Обозначим буквами \(S\) и \(S_1\) площади этих треугольников соответственно.
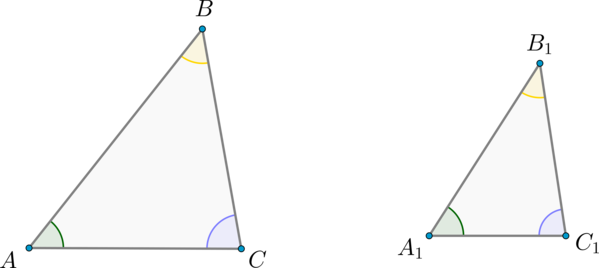
Так как \(\angle A = \angle A_1\), то \(\dfrac{S}{S_1} = \dfrac{AB\cdot
AC}{A_1B_1\cdot A_1C_1}\) (по теореме об отношении площадей треугольников, имеющих по равному углу).
Так как \(\dfrac{AB}{A_1B_1} = \dfrac{AC}{A_1C_1} = k\), то \(\dfrac{S}{S_1} = \dfrac{AB}{A_1B_1}\cdot\dfrac{AC}{A_1C_1} = k\cdot k = k^2\), что и требовалось доказать.
\[{\Large{\text{Признаки подобия треугольников}}}\]
Теорема (первый признак подобия треугольников)
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство
Пусть \(ABC\) и \(A_1B_1C_1\) – треугольники такие, что \(\angle A =
\angle A_1\), \(\angle B = \angle B_1\). Тогда по теореме о сумме углов треугольника \(\angle C = 180^\circ - \angle A - \angle B = 180^\circ
- \angle A_1 - \angle B_1 = \angle C_1\), то есть углы треугольника \(ABC\) соответственно равны углам треугольника \(A_1B_1C_1\).
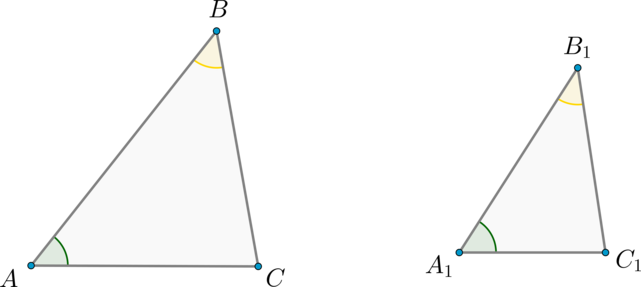
Так как \(\angle A = \angle A_1\) и \(\angle B = \angle B_1\), то \(\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot AC}{A_1B_1\cdot
A_1C_1}\) и \(\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot
BC}{A_1B_1\cdot B_1C_1}\).
Из этих равенств следует, что \(\dfrac{AC}{A_1C_1} =
\dfrac{BC}{B_1C_1}\).
Аналогично доказывается, что \(\dfrac{AC}{A_1C_1} =
\dfrac{AB}{A_1B_1}\) (используя равенства \(\angle B = \angle B_1\), \(\angle C = \angle C_1\)).
В итоге, стороны треугольника \(ABC\) пропорциональны сходственным сторонам треугольника \(A_1B_1C_1\), что и требовалось доказать.
Теорема (второй признак подобия треугольников)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Доказательство
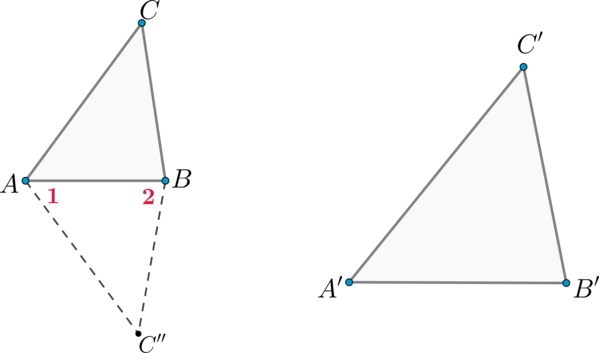
Рассмотрим два треугольника \(ABC\) и \(A'B'C'\), таких что \(\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}\), \(\angle BAC = \angle A'\). Докажем, что треугольники \(ABC\) и \(A'B'C'\) – подобны. Учитывая первый признак подобия треугольников, достаточно показать, что \(\angle B = \angle B'\).
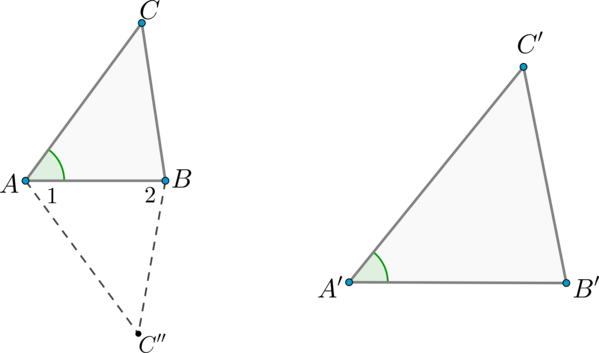
Рассмотрим треугольник \(ABC''\), у которого \(\angle 1 = \angle A'\), \(\angle 2 = \angle B'\). Треугольники \(ABC''\) и \(A'B'C'\) подобны по первому признаку подобия треугольников, тогда \(\dfrac{AB}{A'B'} =
\dfrac{AC''}{A'C'}\).
С другой стороны, по условию \(\dfrac{AB}{A'B'} = \dfrac{AC}{A'C'}\). Из последних двух равенств следует, что \(AC = AC''\).
Треугольники \(ABC\) и \(ABC''\) равны по двум сторонам и углу между ними, следовательно, \(\angle B = \angle 2 = \angle B'\).
Теорема (третий признак подобия треугольников)
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Доказательство
Пусть стороны треугольников \(ABC\) и \(A'B'C'\) пропорциональны: \(\dfrac{AB}{A'B'} = \dfrac{AC}{A'C'} = \dfrac{BC}{B'C'}\). Докажем, что треугольники \(ABC\) и \(A'B'C'\) подобны.
Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что \(\angle BAC = \angle A'\).
Рассмотрим треугольник \(ABC''\), у которого \(\angle 1 = \angle A'\), \(\angle 2 = \angle B'\).
Треугольники \(ABC''\) и \(A'B'C'\) подобны по первому признаку подобия треугольников, следовательно, \(\dfrac{AB}{A'B'} = \dfrac{BC''}{B'C'}
= \dfrac{C''A}{C'A'}\).
Из последней цепочки равенств и условия \(\dfrac{AB}{A'B'} =
\dfrac{AC}{A'C'} = \dfrac{BC}{B'C'}\) вытекает, что \(BC = BC''\), \(CA
=
C''A\).
Треугольники \(ABC\) и \(ABC''\) равны по трем сторонам, следовательно, \(\angle BAC = \angle 1 = \angle A'\).

\[{\Large{\text{Теорема Фалеса}}}\]
Теорема
Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
Доказательство
Докажем сначала лемму: Если в \(\triangle OBB_1\) через середину \(A\) стороны \(OB\) проведена прямая \(a\parallel BB_1\), то она пересечет сторону \(OB_1\) также в середине.
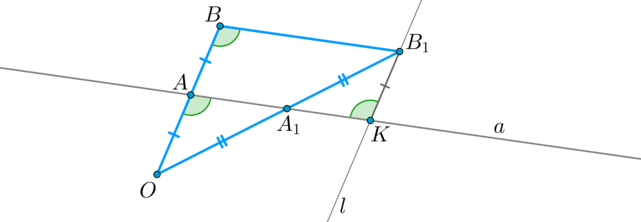
Через точку \(B_1\) проведем \(l\parallel OB\). Пусть \(l\cap a=K\). Тогда \(ABB_1K\) — параллелограмм, следовательно, \(B_1K=AB=OA\) и \(\angle
A_1KB_1=\angle ABB_1=\angle OAA_1\); \(\angle AA_1O=\angle KA_1B_1\) как вертикальные. Значит, по второму признаку \(\triangle
OAA_1=\triangle B_1KA_1 \Rightarrow OA_1=A_1B_1\). Лемма доказана.
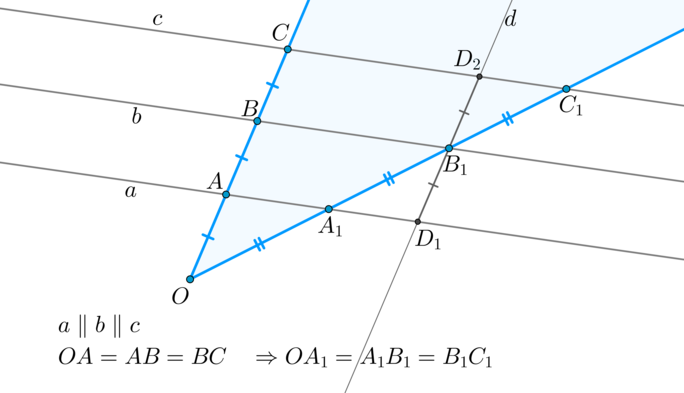
Перейдем к доказательству теоремы. Пусть \(OA=AB=BC\), \(a\parallel
b\parallel c\) и нужно доказать, что \(OA_1=A_1B_1=B_1C_1\).
Таким образом, по данной лемме \(OA_1=A_1B_1\). Докажем, что \(A_1B_1=B_1C_1\). Проведем через точку \(B_1\) прямую \(d\parallel OC\), причем пусть \(d\cap a=D_1, d\cap c=D_2\). Тогда \(ABB_1D_1, BCD_2B_1\) — параллелограммы, следовательно, \(D_1B_1=AB=BC=B_1D_2\). Таким образом, \(\angle A_1B_1D_1=\angle C_1B_1D_2\) как вертикальные, \(\angle
A_1D_1B_1=\angle C_1D_2B_1\) как накрест лежащие, и, значит, по второму признаку \(\triangle A_1B_1D_1=\triangle C_1B_1D_2
\Rightarrow A_1B_1=B_1C_1\).
Теорема Фалеса
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
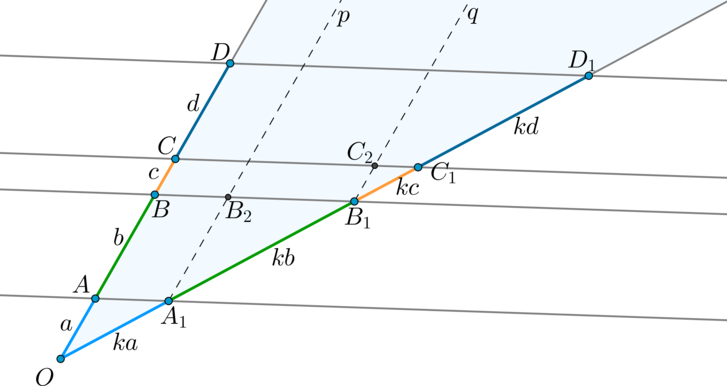
Доказательство
Пусть параллельные прямые \(p\parallel q\parallel r\parallel s\) разбили одну из прямых на отрезки \(a, b, c, d\). Тогда вторую прямую эти прямые должны разбить на отрезки \(ka, kb, kc, kd\) соответственно, где \(k\) – некоторое число, тот самый коэффициент пропорциональности отрезков.
Проведем через точку \(A_1\) прямую \(p\parallel OD\) (\(ABB_2A_1\) — параллелограмм, следовательно, \(AB=A_1B_2\)). Тогда \(\triangle OAA_1
\sim \triangle A_1B_1B_2\) по двум углам. Следовательно, \(\dfrac{OA}{A_1B_2}=\dfrac{OA_1}{A_1B_1} \Rightarrow A_1B_1=kb\).
Аналогично проведем через \(B_1\) прямую \(q\parallel OD \Rightarrow
\triangle OBB_1\sim \triangle B_1C_1C_2 \Rightarrow B_1C_1=kc\) и т.д.

\[{\Large{\text{Средняя линия треугольника}}}\]
Определение
Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.
Теорема
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Доказательство
1) Параллельность средней линию основанию следует из доказанной выше леммы.
2) Докажем, что \(MN=\dfrac12 AC\).
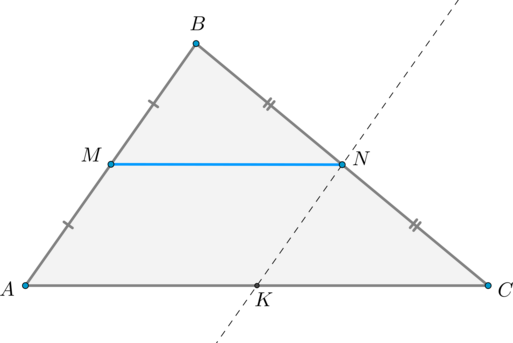
Через точку \(N\) проведем прямую параллельно \(AB\). Пусть эта прямая пересекла сторону \(AC\) в точке \(K\). Тогда \(AMNK\) — параллелограмм (\(AM\parallel NK, MN\parallel AK\) по предыдущему пункту). Значит, \(MN=AK\).
Т.к. \(NK\parallel AB\) и \(N\) – середина \(BC\), то по теореме Фалеса \(K\) – середина \(AC\). Следовательно, \(MN=AK=KC=\dfrac12 AC\).
Следствие
Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом \(\frac12\).













