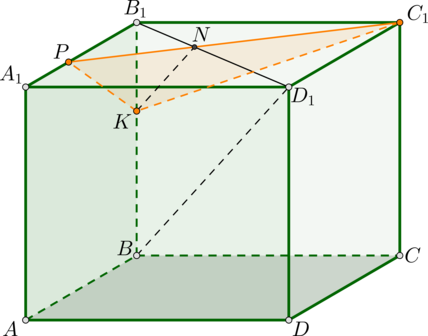
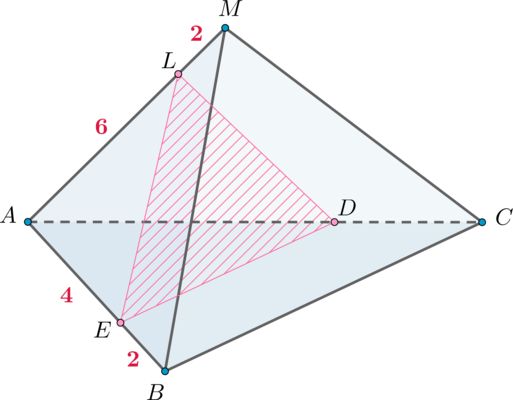
Основанием прямой четырехугольной призмы \(ABCDA_1B_1C_1D_1\) является квадрат \(ABCD\) со стороной \(3\sqrt2\), высота призмы равна \(2\sqrt7\). Точка \(K\) – середина ребра \(BB_1\). Через точки \(K\) и \(C_1\) проведена плоскость \(\alpha\), параллельная прямой \(BD_1\).
а) Докажите, что сечение призмы плоскостью \(\alpha\) является равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью \(\alpha\).
(ЕГЭ 2015, резервный день)
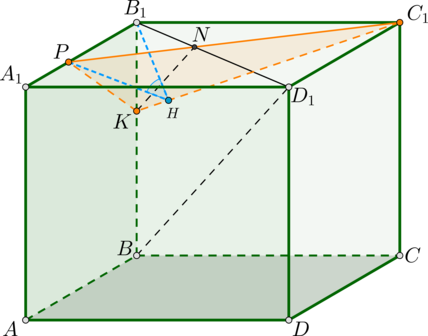
а) Прямая параллельна плоскости, если плоскость содержит прямую, параллельную данной. Поэтому проведем в плоскости \(BB_1D_1\), содержащей \(BD_1\), прямую \(KO\parallel BD_1\). Пусть \(O\) – точка пересечения с отрезком \(B_1D_1\).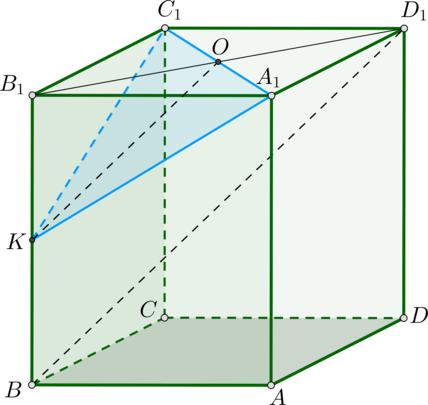
Т.к. \(KO\parallel BD_1\), то по теореме Фалеса
\[\dfrac{B_1O}{OD_1}=\dfrac{B_1K}{KB}=1.\]
Следовательно, \(O\) – середина \(B_1D_1\). Т.к. \(A_1B_1C_1D_1\) – квадрат, то его диагонали точкой пересечения делятся пополам, следовательно, \(A_1C_1\) содержит \(O\).
Таким образом, \(A_1KC_1\) – искомое сечение. Из равенства боковых граней следует, что отрезки \(KC_1\) и \(KA_1\) равны, то есть треугольник \(A_1KC_1\) равнобедренный.
б) Найдем по теореме Пифагора \(KA_1\):
\[KA_1=\sqrt{KB_1^2+B_1A_1^2}=\sqrt{(\sqrt7)^2+(3\sqrt2)^2}=5.\]
Диагональ квадрата равна стороне квадрата, умноженной на \(\sqrt2\), следовательно, \(A_1C_1=A_1B_1\cdot \sqrt2=6\).
Таким образом, периметр
\[P_{A_1KC_1}=5+5+6=16.\]
Ответ:
б) \(16\)