Свойства квадратичной функции (страница 2)

Графиком функции \(y_1=x^2+ax\) является парабола, ветви которой направлены вверх, и которая имеет либо одну точку пересечения с осью абсцисс (если \(a=0\)), либо две точки пересечения с осью абсцисс: \((a;0)\) и \((0;0)\) (если \(a \ne 0\)).

При \(a=0\) функции принимают вид: \(y=|x^2|=x^2\) и \(y=0\). Для того, чтобы найти точки пересечения графиков функций, можно решить уравнение \(x^2=0\). Это уравнение имеет один корень, следовательно, \(a=0\) не подходит.

Пусть \(a\ne 0\). Значит, графиком \(y=|x^2+ax|\) является:

Для того, чтобы графики функций имели три общие точки, необходимо, чтобы прямая \(y=2a\) выглядела, как показано на рисунке, то есть проходила через вершину \((x_0;y_2(x_0))\) параболы \(y_2=-(x^2+ax)\). Значит:

\[x_0=-\dfrac a2 \quad \Rightarrow \quad y_2(x_0)=\dfrac{a^2}4 \quad \Rightarrow \quad \dfrac{a^2}4=2a\quad \Rightarrow\quad a=8\]

Ответ:

\(a\in \{8\}\)

Перепишем неравенство в виде \((a-1)(a+3)x^2-(3a+1)x+2 \geqslant 0\).

Рассмотрим следующие случаи:

1) \((a-1)(a+3)=0\). В этом случае неравенство становится линейным:

\[\left[ \begin{gathered} \begin{aligned} &\begin{cases} a=1\\[1ex] x\leqslant \frac12 \end{cases}\\[1ex] &\begin{cases} a=-3\\[1ex] x\geqslant -\dfrac{1}{4} \end{cases} \end{aligned} \end{gathered} \right.\]

Видим, что только при \(a=-3\) решение неравенства содержит отрезок \([1;4]\). Следовательно, \(a=-3\) пойдет в ответ.

2) \((a-1)(a+3)>0 \Rightarrow a\in (-\infty;-3)\cup(1;+\infty)\).

В этом случае неравенство является квадратичным, причем при каждом фиксированном \(a\) графиком \(f(x)=(a-1)(a+3)x^2-(3a+1)x+2\) является парабола, ветви которой направлены вверх.

Рассмотрим уравнение \((a-1)(a+3)x^2-(3a+1)x+2=0\): \(D=a^2-10a+25=(a-5)^2\).

2.1) При \(a=5\) (т.е. \(D=0\)) парабола \(f(x)\) имеет ровно одну точку пересечения с осью \(Ox\). Тогда решением неравенства являются все \(x\in \mathbb{R}\), что в свою очередь содержит отрезок \([1;4]\):



Следовательно, \(a=5\) пойдет в ответ.

2.2) При \(a\in (-\infty;-3)\cup(1;5)\cup(5;+\infty)\) (т.е. \(D>0\)) парабола \(f(x)\) имеет две точки пересечения с осью \(Ox\):

\(x_1=\dfrac{3a+1-|a-5|}{2(a-1)(a+3)}\), \(\quad x_2=\dfrac{3a+1+|a-5|}{2(a-1)(a+3)}\)

и решением неравенства являются \(x\in (-\infty;x_1]\cup[x_2;+\infty)\).

Для того, чтобы решение содержало отрезок \([1;4]\), необходимо, чтобы парабола выглядела одним из двух способов:

\[\begin{cases} a\in (-\infty;-3)\cup(1;5)\cup(5;+\infty)\\ \left[ \begin{gathered} \begin{aligned} &x_1\geqslant 4\\ &x_2\leqslant 1 \end{aligned} \end{gathered} \right. \end{cases} \quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &\begin{cases} a\in (-\infty;-3)\cup(1;5)\\[1ex] \left[\begin{gathered} x_1=\dfrac{3a+1+a-5}{2(a-1)(a+3)}\geqslant 4\\[2ex] x_2=\dfrac{3a+1-a+5}{2(a-1)(a+3)}\leqslant 1 \end{gathered}\right. \end{cases} \\[1ex] &\begin{cases} a\in (5;+\infty)\\[1ex] \left[\begin{gathered} x_1=\dfrac{3a+1-a+5}{2(a-1)(a+3)}\geqslant 4\\[2ex] x_2=\dfrac{3a+1+a-5}{2(a-1)(a+3)}\leqslant 1 \end{gathered}\right. \end{cases} \end{aligned}\end{gathered}\right.\] (при \(a<5\) модуль \(|a-5|\) раскрывается отрицательно: \(|a-5|=-(a-5)\), при \(a>5\) он раскрывается положительно: \(|a-5|=a-5\))

Решением данной совокупности будут: \[a\in (-\infty;-3)\cup[2;5)\cup(5;+\infty)\]

3) \((a-1)(a+3)<0 \Rightarrow a\in (-3;1)\). Тогда неравенство также является квадратичным и \(f(x)\) – парабола, ветви которой направлены вниз.

При этих значениях \(a\) также дискриминант \(D>0\), но решением неравенства уже будут \(x\in [x_1;x_2]\). Для того, чтобы решение содержало отрезок \([1;4]\), необходимо, чтобы парабола выглядела так:

\[\begin{cases} a\in (-3;1)\\ f(1)\geqslant 0\\ f(4)\geqslant 0 \end{cases} \Rightarrow a\in (-3;-\dfrac52\Big]\]

Объединяя полученные ранее значения для \(a\), получим окончательный ответ.

Ответ:

\(a\in \left(-\infty;-\frac52\right]\cup[2;+\infty)\).

Данное уравнение с помощью замены \(\cos^2x=t\) сводится к квадратному:

\[t^2-(a-2)t-3(a+1)=0\qquad (*)\]

Заметим, что т.к. \(-1\leqslant \cos x\leqslant 1\), то \(0\leqslant \cos^2x\leqslant 1\). Найдем значения \(a\), при которых уравнение \((*)\) не имеет решений. Тогда все остальные значения \(a\) пойдут в ответ.
Для этого нужно, чтобы парабола \(y=t^2-(a-2)t-3(a+1)\) (заметим, что ее ветви всегда направлены вверх) выглядела одним из следующих способов:



Рис. 1: \(D<0\), уравнение не имеет корней;
Рис. 2: \(D=0\), уравнение имеет один корень \(x=\frac{a-2}2\), который находится либо левее \(0\), либо правее \(1\);
Рис. 3: \(D>0\), уравнение имеет два корня, причем оба корня находятся либо левее \(0\), либо правее \(1\); либо один левее \(0\), а другой правее \(1\).

Все эти случаи записываются следующим образом:

\[\left[ \begin{gathered} \begin{aligned} &D<0\\ &\begin{cases} D=0\\ \left[ \begin{gathered} \begin{aligned} &\dfrac{a-2}2<0\\ &\dfrac{a-2}2>1 \end{aligned} \end{gathered} \right. \end{cases}\\ &\begin{cases} D>0\\ x_{\text{в}}=\dfrac{a-2}2<0\\ y(0)>0 \end{cases}\\ &\begin{cases} D>0\\ x_{\text{в}}=\dfrac{a-2}2>1\\ y(1)>0 \end{cases}\\ &\begin{cases} D>0\\ y(0)<0\\ y(1)<0 \end{cases} \end{aligned} \end{gathered} \right.\]

где \(x_{\text{в}}\) — абсцисса вершины параболы, дискриминант \(D=(a+4)^2\).

Решив данную совокупность, получим: \(a\in (-\infty;-1)\cup(0;+\infty)\). Следовательно, в ответ пойдет \(-1\leqslant a\leqslant 0\).

Ответ:

\(a\in[-1;0]\)

Для того, чтобы данное уравнение имело 4 различных корня, нужно, чтобы каждое из уравнений \(x^2-6x+a-10=0\) и \(x^2-6x-2a+3=0\) имело 2 корня, причем все 4 корня были различны. Пусть \(x_1<x_2\) – корни первого уравнения, \(x_3<x_4\) – корни второго. Следовательно, дискриминанты обоих уравнений положительны: \[\begin{cases} D_1=76-4a>0\\D_2=24+8a>0\end{cases} \quad\Leftrightarrow\quad -3<a<19.\]

Рассмотрим функции \(y_1=x^2-6x+a-10\) и \(y_2=x^2-6x-2a+3\). Графиками этих функций являются параболы, причем обе параболы имеют абсциссу вершины \(x_0=3\). Тогда существует только два возможных варианта расположения корней.

1) График \(y_1\) находится выше графика \(y_2\).

Тогда \(x_3<x_1<x_2<x_4\). Т.к. обе параболы симметричны относительно прямой \(x=3\), то точки \(x_1\) и \(x_2\) находятся на одинаковом расстояние от точки \(x=3\). Аналогично с точками \(x_3\) и \(x_4\). Учитывая еще то, что они должны образовывать арифметическую прогрессию (то есть расстояние между двумя соседними точками должно быть одинаково, например, \(d>0\)), то \[\begin{cases} x_3=3-\frac32d\\ x_1=3-\frac12d\\ x_2=3+\frac12d\\ x_4=3+\frac32d\end{cases}\]

Т.к. из квадратных уравнений следует, что \(x_1x_2=a-10\), \(x_3x_4=3-2a\), то получаем систему: \[\begin{cases} \left(3-\frac12d\right)\cdot \left(3+\frac12d\right)=a-10\\ \left(3-\frac32d\right)\cdot \left(3+\frac32d\right)=3-2a \end{cases}\]

Решая данную систему, находим, что \(a=15\) – входит в промежуток \((-3;19)\).

2) График \(y_1\) находится ниже графика \(y_2\).

Тогда \(x_1<x_3<x_4<x_2\). Рассуждая аналогично пункту 1, находим \(a=-\dfrac{35}{19}\) – входит в промежуток \((-3;19)\).

Ответ:

\(a\in \left\{-\frac{35}{19};15\right\}\)

Преобразуем данную систему:

\[\begin{cases} \sqrt{xy+2x}=x+1\\ x+1>0\\ \left[\begin{gathered}\begin{aligned} &y-ax-a=2\\ &y-ax-a=-2\end{aligned}\end{gathered}\right.\end{cases} \quad\Leftrightarrow\quad \begin{cases} xy+2x=(x+1)^2\\ x>-1\\ \left[\begin{gathered}\begin{aligned} &y=ax+a+2\\ &y=ax+a-2\end{aligned}\end{gathered}\right.\end{cases}\]

Данная система при \({\color{red}{x>-1}}\) равносильна системе:

\[\left[\begin{gathered}\begin{aligned} &\begin{cases} x^2-xy+1=0\\ y=ax+a+2 \end{cases}\\ &\begin{cases} x^2-xy+1=0\\ y=ax+a-2\end{cases}\end{aligned}\end{gathered}\right. \quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &\begin{cases} (1-a)x^2-(a+2)x+1=0\qquad (1)\\ y=ax+a+2 \end{cases}\\ &\begin{cases} (1-a)x^2-(a-2)x+1=0\qquad (2)\\ y=ax+a-2\end{cases}\end{aligned}\end{gathered}\right.\]

Заметим, что решения первой и второй системы из данной совокупности всегда будут различны, т.к. \(ax+a+2\ne ax+a-2\) при всех \(x\) и \(a\).

I. При \(a=1\) уравнения (1) и (2) – линейные, имеющие корни \(x=\frac13\) и \(x=-1\) соответственно. Но т.к. \(x>-1\), то система не будет иметь два решения.
Следовательно, данное значение \(a\) нам не подходит.

При \(a\ne 1\) уравнения (1) и (2) являются квадратными. Найдем их дискриминанты:

\[D_{(1)}=a^2+8a, \qquad \qquad D_{(2)}=a^2.\]

II. Рассмотрим \(a\in (-\infty;-8)\cup(0;1)\cup(1;+\infty)\).

Тогда \(D_{(1)}>0\) и \(D_{(2)}>0\). Следовательно, оба уравнения имеют по два различных корня.

Корни уравнения (1): \[x_1=\dfrac{a+2\pm \sqrt{D_{(1)}}}{2(1-a)}, \quad x_1<x_2.\] Корни уравнения (2): \[x_3=-1 \quad \text{и}\quad x_4=\dfrac1{a-1}.\] Т.к. \(x>-1\), то корень \(x_3\) точно не подходит.

Рассмотрим три случая:
\(\bullet\) \(a\in (0;1)\). Тогда \(x_4=\frac1{a-1}\in (-\infty;-1)\). Следовательно, \(x_4\) тоже не подходит.
Тогда для того, чтобы исходная система имела два различных решения, нужно, чтобы \(x_1>-1, x_2>-1\).
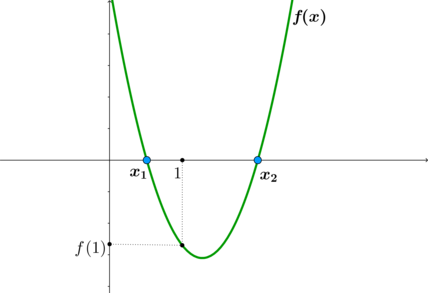
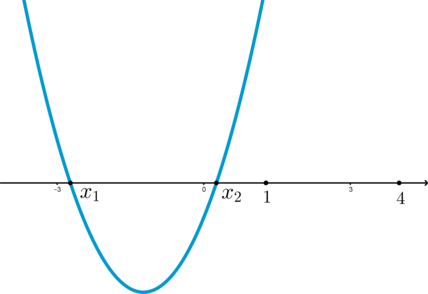
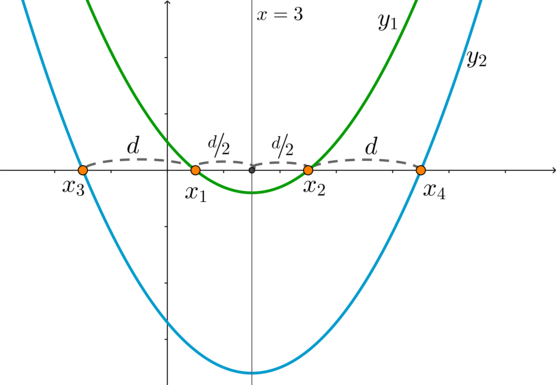
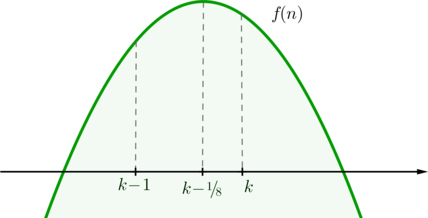
Рассмотрим параболу \(y=(1-a)x^2-(a+2)x+1\). При рассматриваемых \(a\) ее ветви направлены вверх, следовательно, т.к. \(y(-1)=4>0\), то можно сказать, что корни \(x_1\) и \(x_2\) находятся либо одновременно правее \(-1\) (подходит), либо одновременно левее \(-1\) (не подходит).
Для того, чтобы оба были правее \(-1\), нужно, чтобы и вершина параболы была правее \(-1\), то есть \[\dfrac{a+2}{2(1-a)}>-1\quad\Leftrightarrow\quad\dfrac{a-4}{a-1}>0 \quad\Leftrightarrow\quad a\in (-\infty;1)\cup(4;+\infty).\] Пересекая полученные значения с \(a\in (0;1)\), получим \(a\in (0;1)\).

\(\bullet\) \(a\in (-\infty;-8)\). Тогда \(x_4=\frac1{a-1}\in \left(-\frac19;0\right)\). Следовательно, \(x_4\) нам подходит.
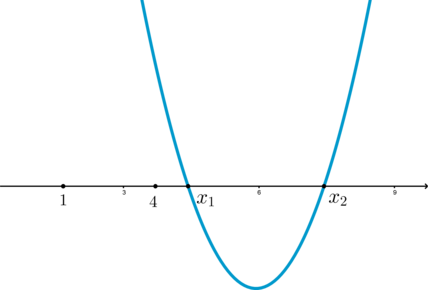
Тогда для того, чтобы исходная система имела два решения, нужно, чтобы \(x_1\leqslant -1\), а \(x_2>-1\).
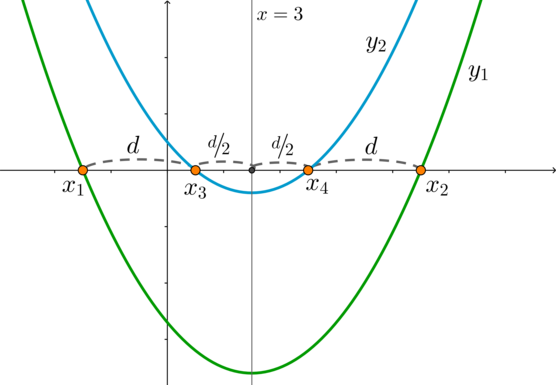
Парабола и в данном случае с ветвями, направленными вверх, следовательно, учитывая \(y(-1)=4>0\), можно сказать, что оба корня \(x_1\) и \(x_2\) находятся либо одновременно левее, либо одновременно правее \(-1\). Такая ситуация нам не подходит.

\(\bullet\) \(a\in (1;+\infty)\). Тогда \(x_4=\frac1{a-1}\in (0;+\infty)\). Следовательно, \(x_4\) нам подходит.
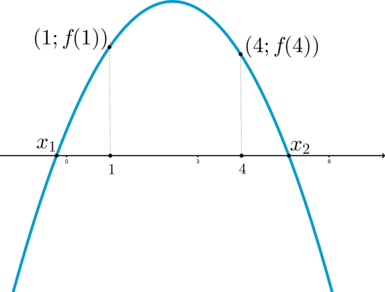
Тогда нужно, чтобы \(x_1\leqslant -1\), а \(x_2>-1\).
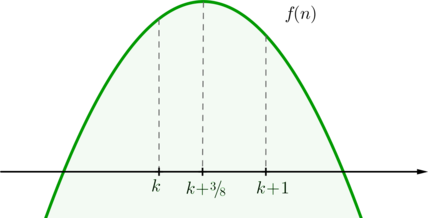
Парабола в данном случае с ветвями вниз, то есть, учитывая \(y(-1)=4>0\), корни находятся по разные стороны от \(-1\). Значит, этот случай нам подходит.

Следовательно, при \(a\in (0;1)\cup(1;+\infty)\) система имеет два решения.

III. При \(a\in (-8;0)\) имеем: \(D_{(1)}<0\) и \(D_{(2)}>0\). Следовательно, уравнение (1) не имеет корней, а уравнение (2) имеет те же два корня \(x_3=-1\) и \(x_4=\frac1{a-1}\), из которых \(x_3\) не подходит под \(x>-1\). Следовательно, мы не получим два решения системы.

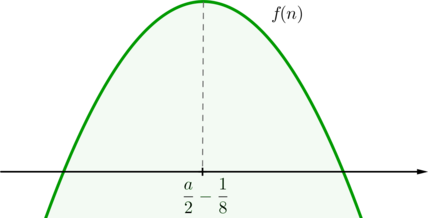
IV. При \(a=-8\) имеем \(D_{(1)}=0\) и \(D_{(2)}>0\). Следовательно, уравнение (1) имеет один корень \(x_1=-\frac13\), уравнение (2) имеет корни \(x_3=-1\) и \(x_4=-\frac19\). Таким образом, учитывая \(x>-1\), система будет иметь два решения:

\[\left(-\frac13;-\frac{10}3\right)\qquad \text{и}\qquad \left(-\dfrac19;-\dfrac{82}9\right).\]

V. При \(a=0\) имеем \(D_{(1)}=0\) и \(D_{(2)}=0\), следовательно, оба уравнения имеют по одному корню: \(x_1=1\) и \(x_3=-1\). Видим, что двух решений система не имеет.

Таким образом, ответ: \(a\in \{-8\}\cup(0;1)\cup(1;+\infty)\).

Ответ:

\(\{-8\}\cup(0;1)\cup(1;+\infty)\)

Сделаем замену для удобства: \(\pi ax=t\). Тогда неравенство примет вид: \[\begin{aligned} &\log_2(\sin t+\cos t)\geqslant \dfrac12 \quad\Leftrightarrow\quad \sin t+\cos t\geqslant \sqrt2 \quad\Leftrightarrow\quad \sqrt2\sin \left(t+\dfrac{\pi}4\right)\geqslant \sqrt2 \quad\Leftrightarrow\\[2ex] & \sin \left(t+\dfrac{\pi}4\right)\geqslant 1 \quad\Leftrightarrow\quad \sin \left(t+\dfrac{\pi}4\right)=1 \quad\Leftrightarrow\quad t+\dfrac{\pi}4=\dfrac{\pi}2+2\pi n, n\in\mathbb{Z} \quad\Leftrightarrow\quad t=\dfrac{\pi}4+2\pi n, n\in\mathbb{Z} \end{aligned}\]

Сделав обратную замену и учитывая, что \(a\ne 0\), получим: \[x=\dfrac 1a \left(\dfrac14+2n\right) , n\in\mathbb{Z}\]

Преобразуем функцию, максимальное значение которой нужно найти: \[f(x)=-x^2+2x-1+1=-(x-1)^2+1\]

Таким образом, функция примет вид: \[f(n)=-\left(\dfrac1a\left(\dfrac14+2n\right)-1\right)^2+1= -\dfrac4{a^2}\left(n+\dfrac18-\dfrac a2\right)^2+1\]

Таким образом, графиком функции при каждом фиксированном значении \(a\) является парабола, ветви которой направлены вниз, а вершина параболы находится в точке \(n_0=\frac a2-\frac18\):

Рассмотрим параболу только при целых \(n\) (так как, вообще говоря, \(n\) – целое). \(n_0=\frac a2-\frac18\) ни при каких целых \(a\) не будет являться целым числом. Следовательно, наибольшее значение функция принимает точно не в вершине.

Рассмотрим два случая:

1) \(a=2k, k\in\mathbb{Z}\,\backslash \{0\}\).

Тогда \(n_0=k-\dfrac18\). Следовательно, парабола выглядит так:

Заметим, что так как парабола симметрична относительно прямой \(n=k-\frac18\), то чем ближе число \(n\) расположено к \(k-\frac18\), тем больше будет значение функции \(f\) в нем. Следовательно, максимальное значение функция \(f(n)\) будет принимать либо при \(n=k-1\), либо при \(n=k\). Заметим, что \(k\) находится ближе к \(k-\frac18\), чем \(k-1\). Таким образом: \[f_{max}=f(k)=f\left(\frac a2\right)=1-\dfrac1{16a^2}\]

2) \(a=2k+1, k\in\mathbb{Z}\).

Тогда \(n_0=k+\dfrac38\). Следовательно, парабола выглядит так:

Аналогично, максимальное значение функция \(f(n)\) будет принимать либо при \(n=k+1\), либо при \(n=k\). Заметим, что \(k\) находится ближе к \(k+\frac38\), чем \(k+1\). Таким образом: \[f_{max}=f(k)=f\left(\frac{a-1}2\right)=1-\dfrac9{16a^2}\]

Ответ:

при \(a\) четном \(f_{max}=1-\dfrac1{16a^2}\)  

при \(a\) нечетном \(f_{max}=1-\dfrac9{16a^2}\)