Работа с внешними углами многоугольника с помощью тригонометрии (страница 2)

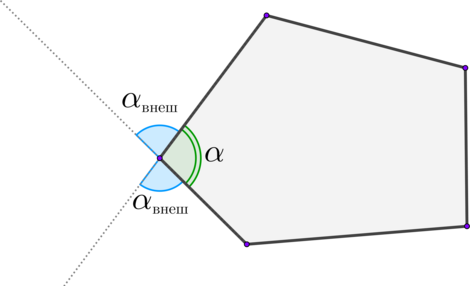
Так как \(AB = BC\), то \(\angle A = \angle C\). Внешний угол треугольника равен сумме углов треугольника, не смежных с ним, тогда внешний угол при вершине \(B\) равен \(2\cdot \angle A\), а его синус равен \(\sin{(2\cdot\angle A)}\).

\[\sin{(2\cdot\angle A)} = 2\sin{\angle A}\cdot \cos{\angle A}.\] При помощи основного тригонометрического тождества находим \(\cos{\angle A} = \pm 0,28\), но в равнобедренном треугольнике угол при основании всегда острый, тогда \(\cos{\angle A} = 0,28\), следовательно, \(\sin{(2\cdot\angle A)} = 2\sin{\angle A}\cdot \cos{\angle A} = 2\cdot 0,96 \cdot 0,28 = 0,5376\).

Ответ: 0,5376

Пусть \(AD\parallel BC\), внешние углы построены как на рисунке (при каждой вершине может быть два внешних угла, но их градусные меры совпадают, а значит, и косинусы этих углов равны и ответ не зависит от выбора угла при каждой вершине).

Сумма внешних углов при вершинах \(A\) и \(B\) равна \(180^{\circ}\) (так как внешний угол при вершине \(A\) и \(\angle ABC\) равны, как внутренние накрест лежащие при параллельных прямых и секущей).

Аналогично сумма внешних углов при вершинах \(C\) и \(D\) равна \(180^{\circ}\).

\[\cos{(180^{\circ} - \alpha)} = -\cos{\alpha} \qquad\Rightarrow\qquad \cos{(180^{\circ} - \alpha)} + \cos{\alpha} = 0,\] следовательно, сумма косинусов внешних углов при вершинах \(A\) и \(B\) равна 0;

аналогично сумма косинусов внешних углов при вершинах \(C\) и \(D\) равна 0. Таким образом, сумма косинусов внешних углов равна 0.

Ответ: 0

Т.к. \(\cos \angle LAE=\frac12 \quad \Rightarrow \quad \angle LAE=60^\circ\). Т.к. \(\sin \angle NAE=\frac12\), то \(\angle NAE\) равен либо \(30^\circ\), либо \(150^\circ\). Но пятиугольник выпуклый, а это значит, что все его внутренние углы меньше \(180^\circ\), следовательно, \(\angle NAE=30^\circ\) и весь \(\angle A=30^\circ +60^\circ=90^\circ\) (иначе весь \(\angle A\) был бы равен \(60^\circ +150^\circ >180^\circ\)).

Значит, и внешний угол при вершине \(A\) равен \(90^\circ\), а его синус таким образом равен \(1\).

Ответ: 1

Т.к. синусы смежных углов равны, то \(\sin \angle O_{\text{внеш}}=\sin \angle O\). Рассмотрим два случая: когда \(\angle O\) – острый и когда тупой. Пусть \(GK\) — та самая высота из условия.

В первом случае из прямоугольного треугольника \(OGK\) \[\cos \angle OGK=\sin \angle O \quad \Rightarrow \quad \sin \angle O_{\text{внеш}}=\cos \angle OGK=0,6\]

Во втором случае из прямоугольного треугольника \(OGK\) \[\cos \angle OGK=\sin \angle O_{\text{внеш}} \quad \Rightarrow \quad \sin \angle O_{\text{внеш}}=0,6.\]

Ответ: 0,6