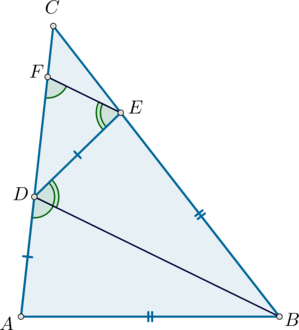
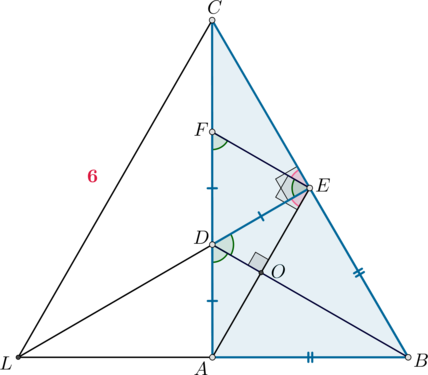
Две окружности касаются внешним образом в точке \(L\). Прямая \(AB\) касается первой окружности в точке \(A\), а второй – в точке \(B\). Прямая \(BL\) пересекает первую окружность в точке \(D\), а прямая \(AL\) пересекает вторую окружность в точке \(C\).
а) Докажите, что прямые \(AD\) и \(BC\) параллельны.
б) Найдите площадь треугольника \(ALB\), если известно, что радиусы окружностей равны \(8\) и \(2\).
а) 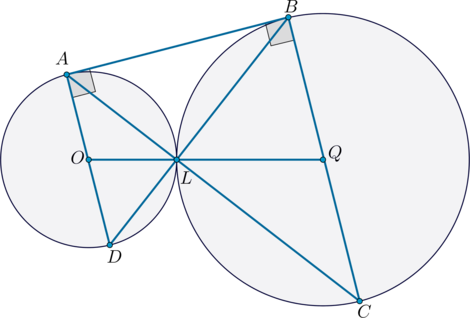
Пусть \(O\) – центр первой окружности, \(Q\) – центр второй. Докажем, что точки \(A, O, D\) лежат на одной прямой (то есть что \(AD\) – диаметр). Так как \(OA\perp AB\), \(QB\perp AB\) (как радиусы, проведенные в точки касания), то \(AO\parallel BQ\). Следовательно, \(\angle AOL+\angle BQL=180^\circ\) как односторонние углы при \(AO\parallel BQ\) и \(OQ\) секущей.
\(\angle BLQ=\angle OLD\) как вертикальные.
Заметим, что \(\triangle BLQ\) и \(\triangle LOD\) – равнобедренные, причем их углы при основании равны, следовательно, равны и углы при вершине: \(\angle LOD=\angle BQL\). Таким образом, \(\angle AOL+\angle
LOD=180^\circ\), следовательно, точки \(A, O, D\) лежат на одной прямой.
Аналогично доказывается, что точки \(B, Q, C\) лежат на одной прямой.
Следовательно, \(AD\perp AB\), \(BC\perp AB\), откуда \(AD\parallel BC\), чтд.
б) 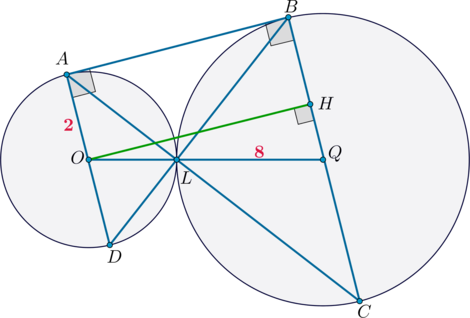
Обозначим \(\angle OLA=\alpha\), \(\angle QLB=\beta\). Тогда \(\angle
AOL=180^\circ-2\alpha\), \(\angle BQL=180^\circ-2\beta\).
Тогда \(180^\circ-2\alpha+180^\circ-2\beta=180^\circ\), откуда \(\alpha+\beta=90^\circ\). Следовательно, \(\angle
ALB=180^\circ-90^\circ=90^\circ\), то есть \(\triangle ALB\) – прямоугольный с гипотенузой \(AB\).
Проведем \(OH\perp BQ\). Тогда \(ABHO\) – прямоугольник (все углы прямые), следовательно, \(HQ=BQ-AO=8-2=6\). Из прямоугольного \(\triangle OHQ\) по теореме Пифагора: \[OH=\sqrt{OQ^2-HQ^2}=8\] Так как \(ABHO\) прямоугольник, то \(AB=OH=8\).
\(\triangle ABC\) также прямоугольный (\(\angle B=90^\circ\)), следовательно, \[AC=\sqrt{AB^2+BC^2}=8\sqrt5\] Заметим, что \(\triangle AOL\sim \triangle CQL\), следовательно, \[\dfrac{AL}{LC}=\dfrac{AO}{CQ}=\dfrac 28\] Следовательно, \[AL=\dfrac15AC=\dfrac8{\sqrt5}\] Тогда по теореме Пифагора из \(\triangle ALB\): \[BL=\sqrt{AB^2-AL^2}=\dfrac{16}{\sqrt5}\] Следовательно, \[S_{ALB}=\dfrac12\cdot AL\cdot BL=\dfrac{64}5\]
Ответ:
б) \(\frac{64}5\)