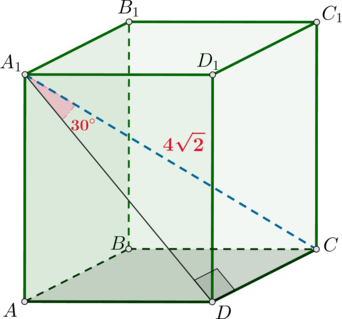
Дана прямая призма \(ABCDA_1B_1C_1D_1\), в основании которой лежит равнобедренная трапеция \(ABCD\), у которой \(AB=BC=CD\), а острый угол при основании \(AD\) равен \(60^\circ\). Пусть \(O\) – точка пересечения продолжений боковых сторон основания призмы. Найдите, отношение объема призмы \(ABCDA_1B_1C_1D_1\) к объему прямой призмы, основанием которой является треугольник \(AOD\), если эти призмы имеют равные высоты.
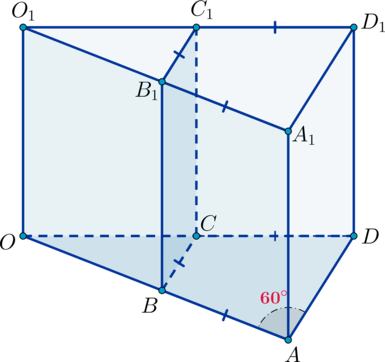
Из условия следует, что нужно найти \[\dfrac{V_{ABCDA_1B_1C_1D_1}}{V_{AODA_1O_1D_1}}\] Так как \(AD\parallel BC\) и трапеция равнобедренная, то \(\angle
OBC=\angle OCB=\angle OAD=60^\circ\). Следовательно, \(\triangle OBC\) равнобедренный с углом при основании \(60^\circ\), значит, равносторонний. Значит, \(OB=OC=BC=AB=CD\). Также \(\triangle
OBC\sim\triangle OAD\), причем коэффициент подобия равен \(\frac12\). Следовательно, \(S_{OBC}=\frac14S_{OAD}\). Тогда \(S_{ABCD}=\frac34S_{OAD}\). Значит \[\dfrac{V_{ABCDA_1B_1C_1D_1}}{V_{AODA_1O_1D_1}}=
\dfrac{AA_1\cdot S_{ABCD}}{AA_1\cdot S_{OAD}}=\dfrac34=0,75.\]
Ответ: 0,75