\(\blacktriangleright\) Для того, чтобы найти наибольшее/наименьшее значение функции на отрезке \([a,b]\), необходимо схематично изобразить график функции на этом отрезке.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания (\(f'>0\)) и убывания (\(f'<0\)) функции, критические точки (где \(f'=0\) или \(f'\) не существует).

\(\blacktriangleright\) Не стоит забывать, что наибольшее/наименьшее значение функция может принимать не только во внутренних точках отрезка \([a,b]\), а также на его концах.

\(\blacktriangleright\) Наибольшее/наименьшее значение функции — это значение координаты \(y=f(x)\).

\(\blacktriangleright\) Производная сложной функции \(f(t(x))\) ищется по правилу: \[{\Large{f'(x)=f'(t)\cdot t'(x)}}\]
\[\begin{array}{|r|c|c|} \hline & \text{Функция } f(x) & \text{Производная } f'(x)\\ \hline \textbf{1} & c & 0\\&&\\ \textbf{2} & x^a & a\cdot x^{a-1}\\&&\\ \textbf{3} & \ln x & \dfrac1x\\&&\\ \textbf{4} & \log_ax & \dfrac1{x\cdot \ln a}\\&&\\ \textbf{5} & e^x & e^x\\&&\\ \textbf{6} & a^x & a^x\cdot \ln a\\&&\\ \textbf{7} & \sin x & \cos x\\&&\\ \textbf{8} & \cos x & -\sin x\\[1ex] \hline \end{array} \quad \quad \quad \quad \begin{array}{|r|c|c|} \hline & \text{Функция } f(x) & \text{Производная } f'(x)\\ \hline \textbf{9} & \mathrm{tg}\, x & \dfrac1{\cos^2 x}\\&&\\ \textbf{10} & \mathrm{ctg}\, x & -\,\dfrac1{\sin^2 x}\\&&\\ \textbf{11} & \arcsin x & \dfrac1{\sqrt{1-x^2}}\\&&\\ \textbf{12} & \arccos x & -\,\dfrac1{\sqrt{1-x^2}}\\&&\\ \textbf{13} & \mathrm{arctg}\, x & \dfrac1{1+x^2}\\&&\\ \textbf{14} & \mathrm{arcctg}\, x & -\,\dfrac1{1+x^2}\\[0.5ex] \hline \end{array}\]

Ознакомиться с полной теорией

Задание 8 #919

Уровень задания: Сложнее ЕГЭ

Найдите наименьшее значение функции \(y = x^{2x}\) на полуинтервале \((0; 0,25]\).

Показать решение

Для положительных \(x\) верно: \(y = e^{2x\cdot \ln x}\).

1) \[y' = (e^{2x\cdot \ln x})' = e^{2x\cdot \ln x}\cdot (2x\cdot \ln x)' = e^{2x\cdot \ln x}\cdot\left(2\ln x + \dfrac{2x}{x}\right) = e^{2x\cdot \ln x}\cdot(2\ln x + 2).\]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[e^{2x\cdot \ln x}\cdot(2\ln x + 2) = 0\qquad\Leftrightarrow\qquad 2\ln x + 2 = 0\] (так как \(e^{t} > 0\) при любом \(t\)), что равносильно \(x = e^{-1}\). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства \(y'\):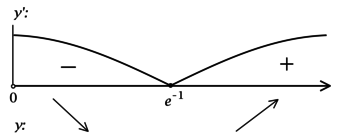

3) Найдём промежутки знакопостоянства \(y'\) на \((0; 0,25]\):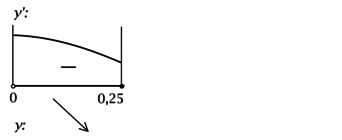

4) Эскиз графика \(y\) на \((0; 0,25]\):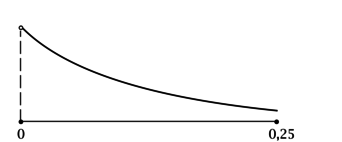

Таким образом, на \((0; 0,25]\) функция \(y\) убывает, следовательно, наименьшее значение достигается в точке \(x = 0,25\):
\(y(0,25) = 0,25^{0,5} = \sqrt{0,25} = 0,5\).

Итого: \(0,5\) – наименьшее значение функции \(y\) на \((0; 0,25]\).

Ответ: 0,5

1 2 cледующая
подтема