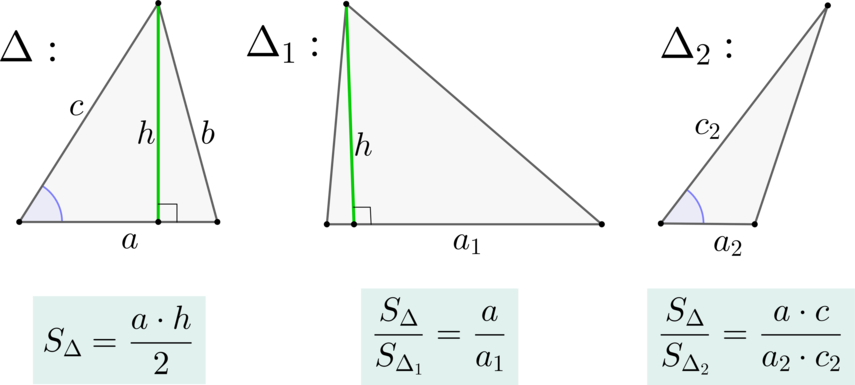
Площадь равнобедренного треугольника \(ABC\) равна \(90\), боковая сторона равна \(10\sqrt{3}\). К основанию \(AB\) и стороне \(BC\) проведены высоты \(CP\) и \(AH\), пересекающиеся в точке \(D\). Найдите площадь треугольника \(CDH\).
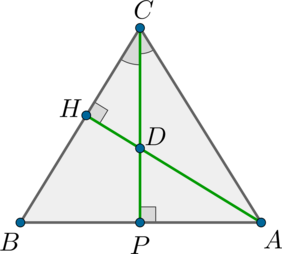
Так как треугольник \(ABC\) равнобедренный, то \(CA = CB=10\sqrt3\), следовательно, \(S_{ABC} = 0,5\cdot CB\cdot AH =
90\quad\Rightarrow\quad AH = 6\sqrt{3}\).
Из треугольника \(HCA\) по теореме Пифагора имеем: \(CH = \sqrt{CA^2 -
AH^2} = 8\sqrt{3}.\)
Так как \(CP\) — высота равнобедренного треугольника \(ABC\), проведенная к основанию \(AB\), то она также является биссектрисой и медианой. Тогда по свойству биссектрисы из \(\triangle HCA\): \[\dfrac{DH}{CH} = \dfrac{DA}{CA} \quad\Rightarrow \quad
\dfrac{DH}{8\sqrt{3}} =\dfrac{(6\sqrt{3} -
DH)}{10\sqrt{3}}\quad\Rightarrow \quad DH = \dfrac{8\sqrt{3}}3\] Следовательно, так как \(\triangle CDH\) прямоугольный, то \(S_{CDH} =
0,5\cdot CH\cdot DH = 32.\)
Ответ: 32