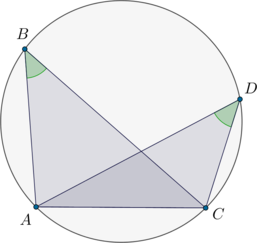
Окружность проходит через вершины \(B\), \(C\) и \(D\) ромба \(ABCD\), причем точка \(A\) находится вне окружности и \(AD\) является касательной к окружности. \(K\) – точка пересечения отрезка \(AC\) и окружности. Найдите отношение \(CK\) к \(KA\).
Рассмотрим картинку: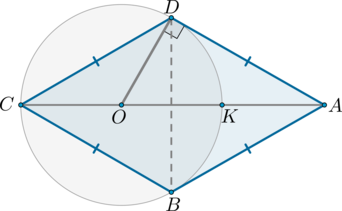
Во-первых, т.к. окружность описана около треугольника \(BCD\), то ее центр \(O\) – точка пересечения серединных перпендикуляров к сторонам треугольника. Следовательно, \(O\) лежит на серединном перпендикуляре к \(BD\) – а это и есть \(CA\) по свойству ромба (диагонали взаимно перпендикулярны). Таким образом, \(CK\) – диаметр этой окружности.
Рассмотрим треугольники \(CDO\) и \(ADK\).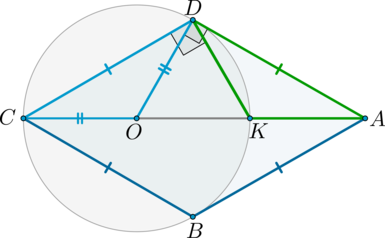
1) Т.к. \(\angle CDK\) опирается на диаметр \(CK\), то он равен \(90^\circ\). Т.к. \(AD\) – касательная к окружности, то угол между ней и радиусом \(OD\) равен \(90^\circ\). Заметим, что углы \(\angle CDK\) и \(\angle ODA\) имеют общую часть – угол \(ODK\). Следовательно, т.к. они равны, то равны и другие их части: \(\angle CDO=\angle ADK=\alpha\).
2) Т.к. треугольник \(CDO\) равнобедренный (\(CO=OD\) – радиусы), то \(\angle DCO=\alpha\). Т.к. треугольник \(CDA\) равнобедренный, то \(\angle DAK=\angle DCO=\alpha\).
3) Таким образом, по стороне и двум прилежащим к ней углам (\(CD=DA, \ \angle DCO=\angle CDO=\angle ADK=\angle DAK\)) треугольники \(CDO\) и \(ADK\) равны. Следовательно, \(KA=CO\).
Значит, \[\dfrac{CK}{KA}=\dfrac{2CO}{CO}=2.\]
Ответ: 2