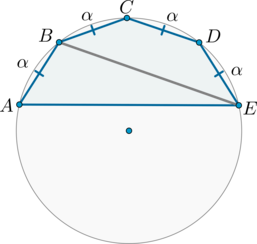
Около пятиугольника \(ABCDE\) описана окружность, причем \(AB=BC=CD=DE=4\sqrt3\), \(\angle A=90^\circ\). Найдите \(AE\).
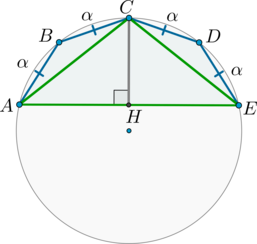
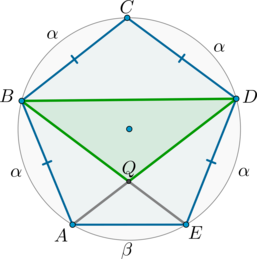
Рассмотрим картинку: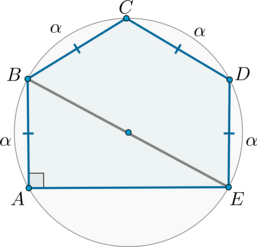
Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги \(\buildrel\smile\over{AB}\), \(\buildrel\smile\over{BC}\), \(\buildrel\smile\over{CD}\), \(\buildrel\smile\over{DE}\) равны:
\[\buildrel\smile\over{AB}=\buildrel\smile\over{BC}= \buildrel\smile\over{CD}=\buildrel\smile\over{DE}=\alpha.\]
Следовательно, \(\angle A=90^\circ=\frac32\alpha\), откуда \(\alpha=60^\circ\).
Значит, вписанный \(\angle AEB=\frac12\alpha=30^\circ\). Следовательно, из прямоугольного треугольника \(AEB\)
\[\mathrm{tg}\,30^\circ=\dfrac{AB}{AE} \quad \Rightarrow \quad AE=12.\]
Ответ: 12