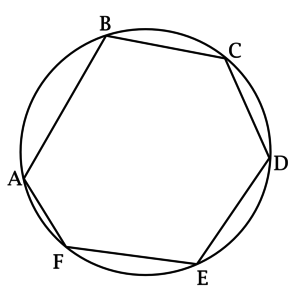
Треугольники \(ABC\) и \(ADC\) имеют общее основание, \(\angle ABC = \angle ADC\), \(M\) – точка пересечения \(AD\) и \(BC\), \(AM = 10\), \(MD = 6\), \(BM = 8\). Найдите \(MC\).
Так как \(\angle ABC = \angle ADC\), то около четырёхугольника \(ABDC\) можно описать окружность. Покажем это: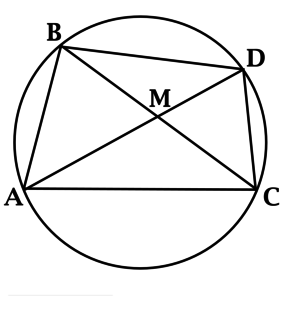
\(\angle AMB\) и \(\angle DMC\) – вертикальные, тогда \(\angle AMB = \angle DMC\); \(\angle ABC = \angle ADC\), тогда треугольники \(ABM\) и \(DMC\) – подобны по двум углам, откуда получаем: \[\dfrac{AM}{MC} = \dfrac{BM}{MD},\] но углы \(BMD\) и \(AMC\) также вертикальные, тогда \(\angle BMD = \angle AMC\) и треугольники \(BMD\) и \(AMC\) – подобны, так как если угол одного треугольника равен углу другого треугольника, а стороны, образующие этот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны.
Из подобия получаем: \(\angle CBD = \angle CAD\), \(\angle MCD = BAM\), тогда \(\angle ABC + \angle CBD + \angle ACB + \angle BCD = \angle ABC + \angle CAD + \angle ACB + \angle BAM = 180^{\circ}\), так как это сумма углов треугольника \(ABC\).
Если в выпуклом четырёхугольнике сумма противоположных углов равна \(180^{\circ}\), то около него можно описать окружность, тогда около \(ABDC\) можно описать окружность.
Так как произведение отрезков одной из пересекающихся хорд равно произведению отрезков другой, то \(AM \cdot MD = BM \cdot MC\), то есть \(60 = 8\cdot MC\), откуда \(MC = 7,5\).
Ответ: 7,5