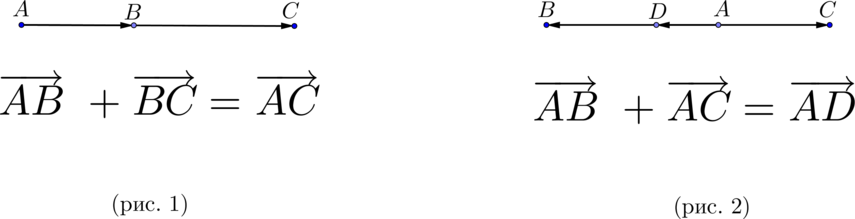Вектор \(\overrightarrow{AB}\) можно рассматривать как перемещение точки из положения \(A\) (начало движения) в положение \(B\) (конец движения). То есть траектория движения в этом случае не важна, важны только начало и конец!

\(\blacktriangleright\) Два вектора коллинеарны, если они лежат на одной прямой или на двух параллельных прямых.
В противном случае векторы называются неколлинеарными.

\(\blacktriangleright\) Два коллинеарных вектора называются сонаправленными, если их направления совпадают.
Если их направления противоположны, то они называются противоположно направленными.

Правила сложения коллинеарных векторов:

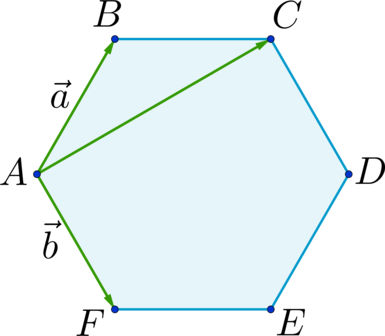
\(\blacktriangleright\) Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).

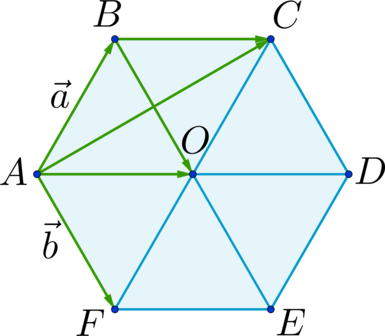
\(\blacktriangleright\) Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).

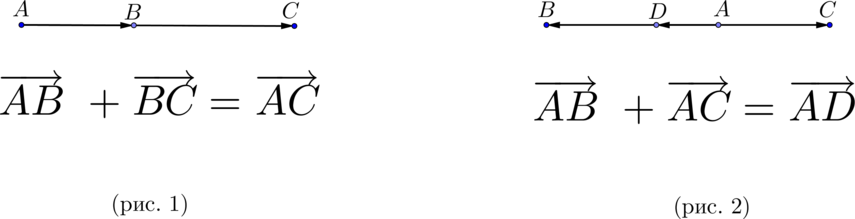
Правила сложения неколлинеарных векторов \(\overrightarrow {a}\) и \(\overrightarrow{b}\):

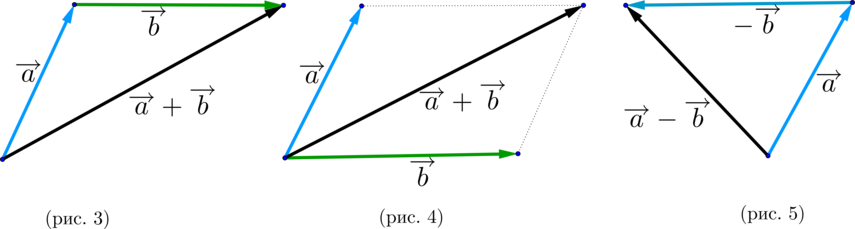
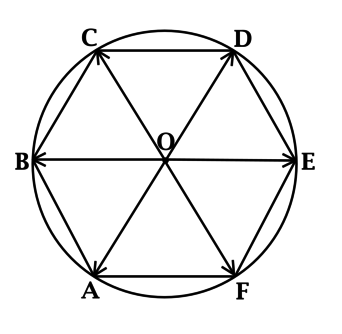
\(\blacktriangleright\) Правило треугольника (рис. 3).

Нужно от конца вектора \(\overrightarrow {a}\) отложить вектор \(\overrightarrow {b}\). Тогда сумма \(\overrightarrow {a}+\overrightarrow {b}\) – это вектор, начало которого совпадает с началом вектора \(\overrightarrow {a}\), а конец – с концом вектора \(\overrightarrow {b}\).

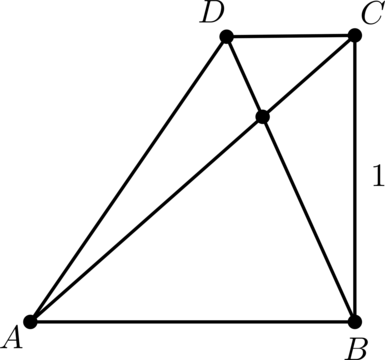
\(\blacktriangleright\) Правило параллелограмма (рис. 4).

Нужно от начала вектора \(\overrightarrow {a}\) отложить вектор \(\overrightarrow {b}\). Тогда сумма \(\overrightarrow {a}+\overrightarrow {b}\) – вектор, совпадающей с диагональю параллелограмма, построенного на векторах \(\overrightarrow {a}\) и \(\overrightarrow {b}\) (начало которого совпадает с началом обоих векторов).

\(\blacktriangleright\) Для того, чтобы найти разность двух векторов \(\overrightarrow {a}-\overrightarrow{b}\), нужно найти сумму векторов \(\overrightarrow {a}\) и \(-\overrightarrow{b}\): \(\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})\) (рис. 5).

Ознакомиться с полной теорией

Задание 8 #1810

Уровень задания: Сложнее ЕГЭ

Дан правильный шестиугольник \(ABCDEF\). Пусть \(\overrightarrow{AB} = \vec{a}\), \(\overrightarrow{AF} = \vec{b}\), тогда \(\overrightarrow{EF} = x\cdot\vec{a} + y\cdot\vec{b}\), где \(x\) и \(y\) – некоторые числа. Найдите число, равное \(x + y\).

Показать решение

Отрезки \(AD\), \(BE\) и \(CF\) пересекаются в точке \(O\) и делятся этой точкой пополам. \(EF \parallel AD\) и \(AOEF\) – параллелограмм; \(AB \parallel FC\) и \(ABOF\) – параллелограмм \(\Rightarrow\) \[\overrightarrow{EF} = \overrightarrow{OA} = \overrightarrow{OF} + \overrightarrow{FA} = \overrightarrow{BA} - \overrightarrow{AF} = - \overrightarrow{AB} - \overrightarrow{AF} = - \vec{a} -\vec{b}\] \(\Rightarrow\) \(x = -1\), \(y = -1\) \(\Rightarrow\) \(x + y = -2\).

Ответ: -2

Задание 9 #1811

Уровень задания: Сложнее ЕГЭ

Дан правильный шестиугольник \(ABCDEF\). Пусть \(\overrightarrow{AB} = \vec{a}\), \(\overrightarrow{AF} = \vec{b}\), тогда \(\overrightarrow{AC} = x\cdot\vec{a} + y\cdot\vec{b}\), где \(x\) и \(y\) – некоторые числа. Найдите число, равное \(x + y\).

Показать решение

\[\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC} = \vec{a} + \overrightarrow{BC}\] Отрезки \(AD\), \(BE\) и \(CF\) пересекаются в точке \(O\) и делятся этой точкой пополам. \(BC \parallel AD\) и \(ABCO\) – параллелограмм; \(AF \parallel BE\) и \(ABOF\) – параллелограмм \(\Rightarrow\) \[\overrightarrow{BC} = \overrightarrow{AO} = \overrightarrow{AB} + \overrightarrow{BO} = \overrightarrow{AB} + \overrightarrow{AF} = \vec{a} + \vec{b}\] \(\Rightarrow\) \[\overrightarrow{AC} = \vec{a} + \vec{a} + \vec{b} = 2\cdot\vec{a} + \vec{b}\] \(\Rightarrow\) \(x = 2\), \(y = 1\) \(\Rightarrow\) \(x + y = 3\).

Ответ: 3

Задание 10 #677

Уровень задания: Сложнее ЕГЭ

\(ABCDEF\) – правильный шестиугольник со стороной длины \(4\), \(O\) – центр описанной около него окружности. Найдите длину вектора \(\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} + \overrightarrow{OE} + \overrightarrow{OF}\).

Показать решение

Опишем около \(ABCDEF\) окружность:

Так как равные хорды стягивают равные дуги, то \[\smile AB = \smile BC = \smile CD = \smile DE = \smile EF = \smile FA,\] тогда \(\smile AFED = \smile ABCD\), следовательно, \(AD\) – диаметр и точки \(A\), \(O\) и \(D\) лежат на одной прямой.
При этом \(AO = OD\) как радиусы, тогда \(\overrightarrow{OA}\) и \(\overrightarrow{OD}\) равны по длине и противоположны по направлению, значит, \(\overrightarrow{OA} = -\overrightarrow{OD}\).

Аналогично \(\overrightarrow{OB} = -\overrightarrow{OE}\) и \(\overrightarrow{OC} = -\overrightarrow{OF}\), тогда
\(\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} + \overrightarrow{OE} + \overrightarrow{OF} = -\overrightarrow{OD} - \overrightarrow{OE} - \overrightarrow{OF} + \overrightarrow{OD} + \overrightarrow{OE} + \overrightarrow{OF} = \vec{0}\).
Нулевой вектор имеет длину равную \(0\).

Ответ: 0

Задание 11 #2660

Уровень задания: Сложнее ЕГЭ

\(ABCD\) – трапеция с основаниями \(AB\) и \(CD\), причём \(\angle ABC = 90^\circ\), \(BC = 1\), \((\vec{AC}, \vec{BD}) = 0,5\). Найдите \((\vec{AB}, \vec{CD})\).

Показать решение

\(\vec{AC} = \vec{AB} + \vec{BC}\), \(\vec{BD} = \vec{BC} + \vec{CD}\)

тогда

\[\begin{aligned} &0,5 = (\vec{AC}, \vec{BD}) = (\vec{AB} + \vec{BC}, \vec{BC} + \vec{CD}) = (\vec{AB} + \vec{BC}, \vec{BC}) + (\vec{AB} + \vec{BC}, \vec{CD}) =\\ & = (\vec{AB}, \vec{BC}) + (\vec{BC}, \vec{BC}) + (\vec{AB}, \vec{CD}) + (\vec{BC}, \vec{CD}) \end{aligned}\]

Так как \(ABCD\) – трапеция, а \(\angle ABC = 90^\circ\), то и \(\angle DCB = 90^\circ\), следовательно, \((\vec{AB}, \vec{BC}) = (\vec{BC}, \vec{CD}) = 0\), тогда \[0,5 = (\vec{AB}, \vec{CD}) + (\vec{BC}, \vec{BC}) = (\vec{AB}, \vec{CD}) + 1\,,\] откуда получаем, что \((\vec{AB}, \vec{CD}) = -0,5\).

Ответ: -0,5

1 2 cледующая
подтема