Внутри острого угла \(\angle XOY\) взяты точки \(M\) и \(N\) так, что \(\angle XON = \angle YOM\). На отрезке \(OX\) выбрана точка \(Q\) так, что \(\angle NQX = \angle MQO\), а на отрезке \(OY\) выбрана точка \(P\) так, что \(\angle NPO = \angle MPY\).
а) Докажите, что треугольники \(MPN\) и \(MQN\) имеют одинаковые периметры.
б) Пусть \(R_1\) и \(R_2\) – радиусы окружностей, описанных около треугольников \(POM\) и \(NOQ\) соответственно. \[\text{Найдите}\ \dfrac{R_1}{R_2},\ \text{если}\ PN = MQ.\]
а) Достаточно показать, что \(MP + PN = MQ + QN\).
На продолжении отрезка \(MQ\) за точку \(Q\) отметим точку \(N'\) так, что \(QN' = QN\). На продолжении отрезка \(MP\) за точку \(P\) отметим точку \(N''\) так, что \(PN'' = PN\).
Пусть \(S\) – точка пересечения \(NN'\) и \(OX\), \(R\) – точка пересечения \(NN''\) и \(OY\).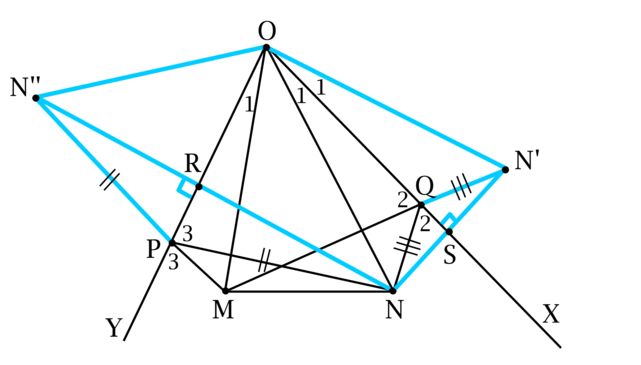
Рассмотрим треугольники \(NQS\) и \(N'QS\): \[\angle NQS = \angle MQO = \angle SQN'\ \text{(как вертикальные)},\qquad NQ = NQ',\qquad QS\ \text{— общая},\] тогда треугольники \(NQS\) и \(N'QS\) равны и \(OX\) – серединный перпендикуляр к \(NN'\).
Так как точка \(O\) лежит на серединном перпендикуляре к \(NN'\), то она равноудалена от точек \(N\) и \(N'\), откуда \(NO = N'O\).
Кроме того, \(OS\) – серединный перпендикуляр, проведённый к основанию равнобедренного треугольника, тогда \(OS\) – биссектриса угла \(\angle NON'\), следовательно, \(\angle SON' = \angle NOS\).
Аналогично \(OY\) – серединный перпендикуляр к \(NN''\), откуда \(N''O = NO\), \(\angle N''OR = \angle RON\).
\[\angle N''OM = \angle N''OR + \angle ROM = \angle RON + \angle SON = \angle MOS + \angle SON' = \angle MON'.\] 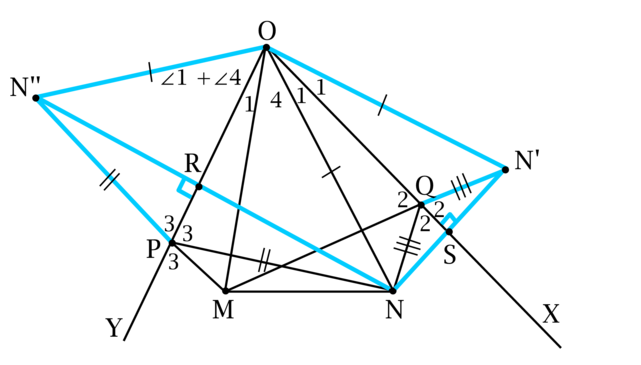
Рассмотрим треугольники \(MN''O\) и \(MNO'\): \[ON'' = ON = ON',\qquad MO\ \text{— общая},\qquad \angle N''OM = \angle MON',\] откуда следует, что треугольники \(MN''O\) и \(MNO'\) равны по двум сторонам и углу между ними. Таким образом, \(MN'' = MN'\), но \[MN'' = MP + PN'' = MP + PN,\qquad MN' = MQ + QN' = MQ + QN,\] откуда получаем требуемое равенство.
Замечание. На рисунке изображена ситуация, когда \(\angle MOY < \angle NOY\), однако, в остальных случаях все рассуждения можно провести абсолютно аналогично.
б) Так как \(MP + PN = MQ + QN\), \(PN = MQ\), то \(MP = QN\).
Из равенства \(MP = QN\) и теоремы синусов получаем: \[2R_1 = \dfrac{MP}{\sin\angle POM} = \dfrac{QN}{\sin\angle NOQ} = 2R_2,\] тогда \(\dfrac{R_1}{R_2} = 1\).
Ответ:
б) \(1\).



