Данное неравенство равносильно:
\(\log_{x^2-3x+2}(a^2x(x-1))>\log_{x^2-3x+2}(x^2-3x+2)
\Rightarrow\quad \) по методу рационализации:
\[\begin{cases}
x^2-3x+2>0\\
x^2-3x+2\ne 1\\
a^2x(x-1)>0\\
(x^2-3x+2-1)(a^2x(x-1)-x^2+3x-2)>0 \end{cases} \Rightarrow\]
\[\begin{cases}
x\in(-\infty;1)\cup(2;+\infty)\\
x\ne \dfrac{3\pm \sqrt5}2\\
x\in (-\infty;0)\cup(1;+\infty)\\
a\ne 0\\
(x^2-3x+1)((a^2-1)x^2-(a^2-3)x-2)>0 \end{cases} \Rightarrow\]
\[\begin{cases}
x\in (-\infty;0)\cup(2;\frac{3+\sqrt5}2)\cup(\frac{3+\sqrt5}2;+\infty)\\
a\ne 0\\
(x^2-3x+1)((a^2-1)x^2-(a^2-3)x-2)>0 \qquad (*)\end{cases}\]
Назовем \(x\in
(-\infty;0)\cup(2;\frac{3+\sqrt5}2)\cup(\frac{3+\sqrt5}2;+\infty)\) — ОДЗ. Рассмотрим последнее неравенство \((*)\).
1) При \(a^2-1=0\) вторая скобка становится линейной и неравенство принимает вид: \[(x^2-3x+1)(x-1)>0 \Rightarrow x\in
\left(\dfrac{3-\sqrt5}2;1\right)\cup
\left(\dfrac{3+\sqrt5}2;+\infty\right)\].
Пересекая данное решение с ОДЗ, получим ответ \(x\in
\left(\dfrac{3+\sqrt5}2;+\infty\right)\), то есть открытый луч.
Значит, значения \(a=-1;1\) нам подходят.
2) Пусть \(a^2-1\ne 0 \), а также \(a\ne 0\) (условие из системы).
Найдем корни уравнения \((a^2-1)x^2-(a^2-3)x-2=0\). \(D=(a^2+1)^2>0\) при любых \(a\).
Следовательно, уравнение всегда имеет два различных корня \(x_1=1; \ x_2=\dfrac2{1-a^2}\).
Тогда выражение можно преобразовать:
\((a^2-1)x^2-(a^2-3)x-2=(a^2-1)(x-\dfrac2{1-a^2})(x-1)=((a^2-1)x+2)(x-1)\).
Для того, чтобы решить неравенство \((x^2-3x+1)((a^2-1)x+2)(x-1)>0\), необходимо рассмотреть два случая: когда \(a^2-1>0\) и \(a^2-1<0\) (от этого зависит первый знак в методе интервалов).
2.1) \(a^2-1>0\). Тогда \(x_2<0\), следовательно, метод интервалов для данного неравенства выглядит так:

Пересекая данное решение с ОДЗ, получим объединение двух открытых лучей: \(x\in (-\infty;x_2)\cup
\left(\frac{3+\sqrt5}2;+\infty\right)\), что нам не подходит.
2.2) \(a^2-1<0\). Тогда \(x_2>0\). Оценим точнее корень \(x_2\):
\(a^2>0 \Rightarrow -a^2<0 \Rightarrow 1-a^2<1\), но в нашем случае также \(a^2-1<0\Rightarrow 1-a^2>0\).
Таким образом, \(0<1-a^2<1
\Rightarrow \dfrac2{1-a^2}>2\).
Таким образом, корень \(x_2\) может располагаться:
а) между \(1\) и \(\dfrac{3+\sqrt5}2\);
б) совпадать с \(\dfrac{3+\sqrt5}2\);
в) быть больше \(\dfrac{3+\sqrt5}2\).
Посмотрим, как будет выглядеть метод интервалов в этих случаях:
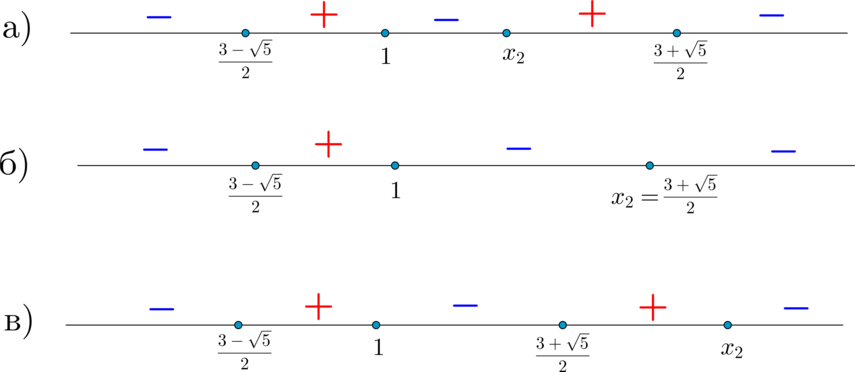
Таким образом, в каждом из случаев а, б, в решение будет выглядеть как интервал или объединение двух интервалов, что после пересечения с ОДЗ не будет лучом. Следовательно, эти случаи нам не подходят.
Ответ:
\(a=\pm 1\)









