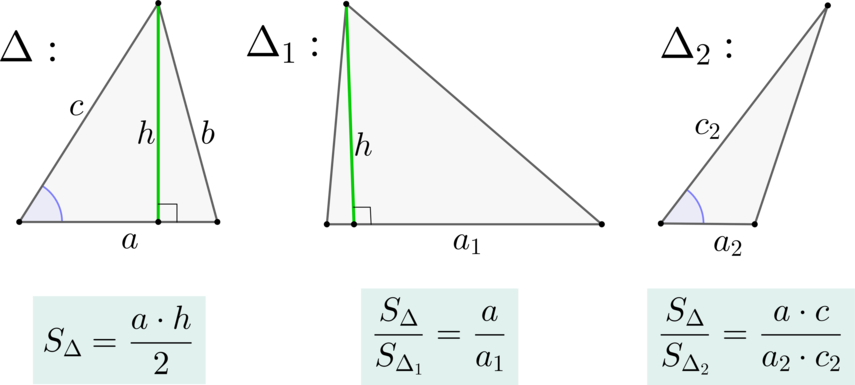
У треугольника со сторонами \(9\) и \(6\) проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна \(4\). Чему равна высота, проведенная ко второй стороне?
Площадь треугольника равна полупроизведению стороны на высоту, проведенную к этой стороне. Следовательно, с одной стороны, \(S=0,5\cdot 9\cdot 4\), а с другой стороны \(S=0,5\cdot 6\cdot h\), где \(h\) – высота, которую нужно найти. Следовательно, \[0,5\cdot 9\cdot 4=0,5\cdot 6\cdot h\quad\Leftrightarrow\quad h=6\]
Ответ: 6