Площадь параллелограмма \(ABCD\) равна \(50\). Найдите площадь выпуклого четырехугольника \(A'B'C'D'\), вершины которого – середины сторон параллелограмма \(ABCD\).
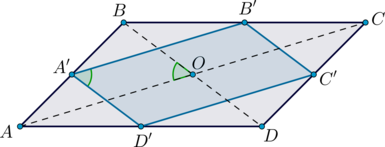
Рассмотрим рисунок. Проведем диагонали \(AC\) и \(BD\). Так как \(A', B'\) – середины \(AB\) и \(BC\), то \(A'B'\) – средняя линия \(\triangle ABC\). Следовательно, \(A'B'=0,5AC\). Аналогично \(C'D'=0,5AC\), \(A'D'=B'C'=0,5BD\). Следовательно, \(A'B'C'D'\) – параллелограмм по признаку.
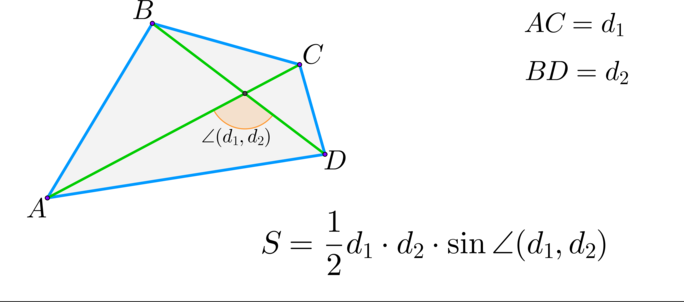
Так как площадь параллелограмма равна полупроизведению диагоналей на синус угла между ними, то \[S_{ABCD}=0,5\cdot AC\cdot BD\cdot \sin\angle AOB\] Так как площадь параллелограмма также можно искать как произведение смежных сторон на синус угла между ними, то \[S_{A'B'C'D'}=A'D'\cdot A'B'\cdot \sin \angle B'A'D'\] Заметим, что \(\angle AOB=\angle B'A'D'\) как углы с попарно параллельными сторонами. Следовательно, \[S_{A'B'C'D'}=0,5BD\cdot 0,5AC\cdot \sin\angle AOB=0,5S_{ABCD}=
0,5\cdot 50=25\]
Ответ: 25