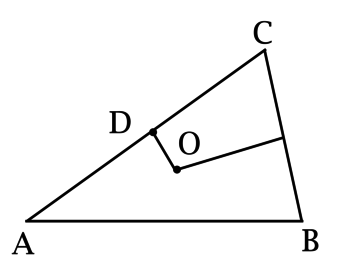
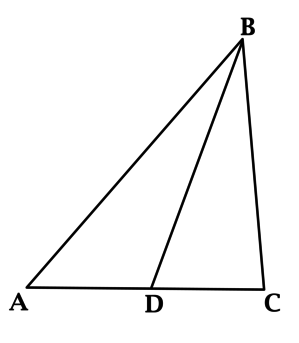
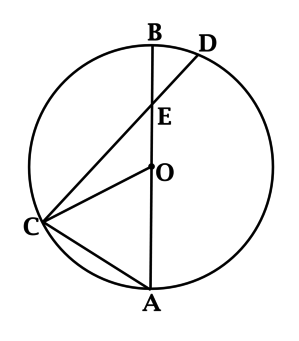
В треугольнике \(ABC\): \(\ O\) – точка пересечения серединных перпендикуляров к сторонам \(AC\) и \(BC = 5\pi < AB\), \(OD = 2,5\pi\) – серединный перпендикуляр к стороне \(CB\). Найдите \(\angle A\). Ответ дайте в градусах.
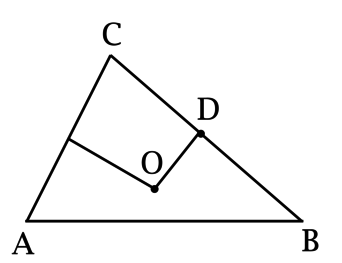
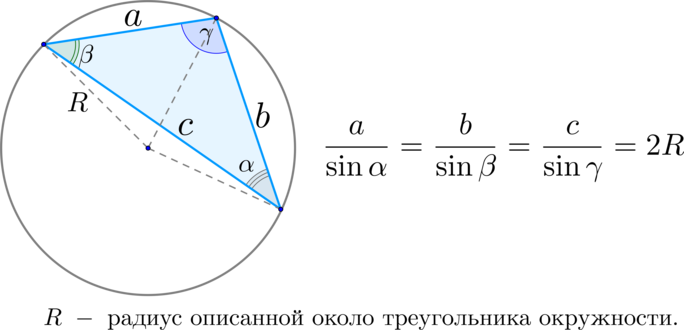
Так как \(O\) – точка пересечения серединных перпендикуляров в треугольнике \(ABC\), то \(O\) – центр описанной около \(ABC\) окружности, \(OC = R\).
По теореме Пифагора \[R^2 = CD^2 + OD^2 = 2\cdot 2,5^2\cdot\pi^2\qquad\Rightarrow\qquad R = 2,5\sqrt{2}\pi\] По теореме синусов \[\dfrac{BC}{\sin\angle A} = 2R \qquad\Rightarrow\qquad \dfrac{5\pi}{\sin\angle A} = 5\sqrt{2}\pi \qquad\Rightarrow\qquad \sin\angle A = \dfrac{1}{\sqrt{2}},\] следовательно, \(\angle A = 45^{\circ}\) или \(\angle A = 135^{\circ}\), но \(AB > BC\), а в треугольнике против большего угла лежит большая сторона, тогда \(\angle A = 45^{\circ}\).
Ответ: 45