Задачи по планиметрии прошлых лет (страница 5)

а) Углы \(\angle CAD\) и \(\angle BCA\) равны как накрест лежащие. Следовательно, т.к. \(\triangle ABC\sim \triangle ACD\), то \(\angle ABC\) равен либо \(\angle ACD\), либо \(\angle ADC\).
Пусть \(\angle ABC=\angle ADC\), тогда \(\angle BAC=\angle ACD\) — накрест лежащие углы при \(AB\) и \(CD\) и секущей \(AC\). То есть \(AB\parallel CD\), что невозможно, т.к. тогда \(ABCD\) – параллелограмм, а не трапеция.
Следовательно, \(\angle ABC=\angle ACD\), чтд.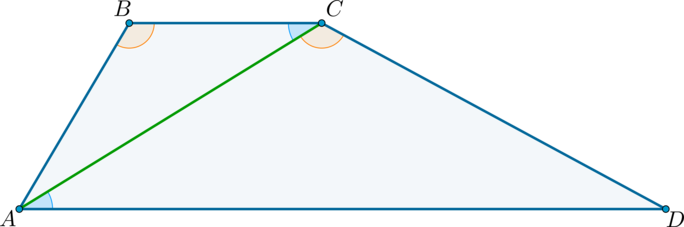

б) Используем условие того, что \(\triangle ABC\sim \triangle ACD\):

\[\dfrac{AC}{AD}=\dfrac{BC}{AC}\quad \Rightarrow\quad AC^2=AD\cdot BC \quad \Rightarrow \quad AC=30.\]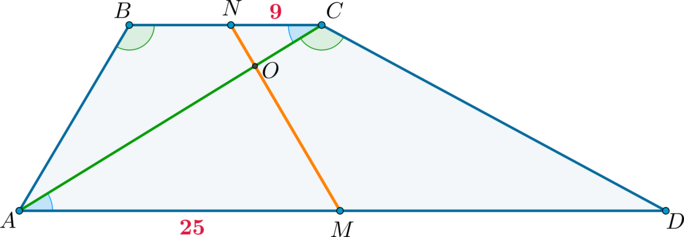

Заметим, что \(\triangle AOM\sim \triangle CON\) с коэффициентом \(\frac{25}9\). Значит, если обозначить \(OC\) за \(k\), то \(AO=\frac{25}9k\). Следовательно, \[AO+OC=\dfrac{34}9k=30 \quad \Rightarrow \quad k=OC=\dfrac{9\cdot 15}{17}.\]

Найдем по теореме косинусов (из условия \(\cos\angle OCN=\cos\angle CAD=\frac35\)) из \(\triangle CON\) \[ON^2=9^2+\left(\dfrac{9\cdot 15}{17}\right)^2- 2\cdot 9\cdot \dfrac{9\cdot 15}{17}\cdot \dfrac35 \quad \Rightarrow \quad ON=\dfrac{9\cdot 4}{17}\cdot \sqrt{13}.\]

Значит, вследствие подобия \[OM=\dfrac{25}9\cdot ON=\dfrac{25\cdot 4}{17}\cdot \sqrt{13}.\]

Таким образом, \[MN=ON+OM=8\sqrt{13}.\]

Ответ:

\(8\sqrt{13}\)

а) Докажем, что \(\angle BAC=\angle BMK\). Из этого будет следовать, что по двум углам \(\triangle ABC\sim \triangle MBK\) (т.к. \(\angle ABC\) у них общий).

Обозначим \(\angle BAC=\alpha\). Тогда \(\angle AHK=90^\circ-\alpha\), следовательно, \(\angle BHK=90^\circ-(90^\circ-\alpha)=\alpha\).
Заметим, что в четырехугольнике \(KBMH\) сумма противоположных углов \(\angle K\) и \(\angle M\) равна \(180^\circ\), следовательно, около него можно описать окружность. Углы \(\angle BHK\) и \(\angle BMK\) — вписанные, опирающиеся на одну и ту же дугу, следовательно, они равны, то есть \(\angle BMK=\alpha\), чтд.

б) Найдем отношение \(S_{\triangle BMK}\) к \(S_{\triangle ABC}\), а из этого уже найдем \(S_{\triangle BMK}\) к \(S_{AKMC}\).

Обозначим \(\angle C=\beta\). Тогда, аналогично первому пункту, \(\angle BHM=\beta\).
Из прямоугольного \(\triangle AHB\):\[\sin\alpha=\dfrac{BH}{AB} \quad \Rightarrow \quad AB=\dfrac{4}{\sin\alpha}.\] Из прямоугольного \(\triangle BHM\): \[\sin\beta=\dfrac{BM}{BH} \quad \Rightarrow \quad BM=4\sin\beta.\] Тогда \[\dfrac{S_{\triangle BMK}}{S_{\triangle ABC}}=\left(\dfrac{BM}{AB}\right)^2=\left(\sin\alpha\cdot \sin\beta\right)^2\]

Найдем \(\sin\alpha\cdot \sin\beta\).
Из формулы, верной для любого треугольника: \[\dfrac{AB}{\sin\angle C}=2R\] следует, что \[\dfrac{\frac4{\sin\alpha}}{\sin\beta}=2\cdot 5 \quad \Rightarrow \quad \sin\alpha\cdot \sin\beta=\dfrac25.\] Таким образом, \[\dfrac{S_{\triangle BMK}}{S_{\triangle ABC}}=\left(\dfrac25\right)^2=\dfrac4{25}.\] Следовательно, \(S_{\triangle BMK}=\dfrac4{25}S_{\triangle ABC}\), откуда \[S_{AKMC}=S_{\triangle ABC}-S_{\triangle BMK}=\frac{21}{25}S_{\triangle ABC}.\] Следовательно, \[S_{\triangle BMK}:S_{AKMC}=4:21.\]

Ответ:

\(\dfrac{4}{21}\)

а)
Из прямоугольного \(\triangle AHB_1\): \[\angle HAB_1=90^\circ-\angle AHB_1.\] Из прямоугольного \(\triangle AA_1C\): \[\angle ACA_1=90^\circ-\angle CAA_1=90^\circ-\angle HAB_1= 90^\circ-(90^\circ-\angle AHB_1)=\angle AHB_1.\] Т.к. \(\angle ACA_1\) и \(\angle ACB\) – одно и то же, то отсюда следует утверждение пункта а).

б) Аналогично пункту а) можно доказать, что \(\angle BAC=\angle B_1HC=30^\circ\).
Тогда из прямоугольного \(\triangle B_1HC\):\[\mathrm{ctg}\,30^\circ=\dfrac{HB_1}{B_1C}.\] Заметим, что \(\triangle AHB_1\sim \triangle BCB_1\) по двум углам. Следовательно, \[\dfrac{AH}{BC}=\dfrac{HB_1}{B_1C}=\mathrm{ctg}\,30^\circ \quad \Rightarrow \quad BC=\dfrac{AH}{\mathrm{ctg}\,30^\circ}=\dfrac{21}{\sqrt3}=7\sqrt3.\]

Ответ:

\(7\sqrt3\)

Данная задача имеет два случая: когда окружности касаются внутренним образом и когда внешним.

1) Пусть окружности касаются внешним образом. Тогда нужно найти площадь четырехугольника \(BO_2CO_1\).

Заметим, что \(\triangle BO_1A\) равнобедренный (\(BO_1=O_1A\) как радиусы), следовательно, \(\angle BO_1A=180^\circ-2\cdot 15^\circ=150^\circ\). Проведем \(BH\perp O_1A\). Тогда \(\angle BO_1H=30^\circ\). Следовательно, \(BH=\frac12BO_1=\frac32\).
Так как \(BH\) — высота \(\triangle BO_1O_2\), опущенная к \(O_1O_2\), то \[S_{BO_1O_2}=\dfrac12BH\cdot O_1O_2.\] Заметим, что \(\triangle CO_2A\sim \triangle BO_1A\) по трем углам (\(\angle BAO_1=\angle CAO_2=15^\circ\) как вертикальные, \(\triangle CO_2A\) тоже равнобедренный). Следовательно, если провести \(CK\perp AO_2\), то \(\angle CO_2K=30^\circ\) и \(CK=\frac12CO_2=\frac52\). Тогда \[S_{CO_2O_1}=\dfrac12CK\cdot O_1O_2\] Следовательно, \[S_{BO_2CO_1}=S_{BO_1O_2}+S_{CO_1O_2}=\dfrac12O_1O_2\cdot (BH+CK)=\dfrac12\cdot (3+5)\cdot \left(\dfrac32+\dfrac52\right)=16.\]

2) Пусть окружности касаются внутренним образом. Тогда необходимо найти площадь четырехугольника \(BO_1O_2C\).

Аналогично \(\triangle BO_1A\sim \triangle CO_2A\) и оба равнобедренные, следовательно, если \(BH\perp AO_2\), то \(BH=\frac12 BO_1=\frac32\), так как \(\angle BO_1A=150^\circ\); а также \(CK=\frac12 CO_2=\frac52\). \[S_{BO_1O_2C}=S_{ACO_2}-S_{ABO_1}=\dfrac12 CK\cdot AO_2-\dfrac12BH\cdot AO_1= \dfrac12\cdot \dfrac52\cdot 5-\dfrac12\cdot \dfrac32\cdot 3=4.\]

Ответ:

4 или 16

Данная задача имеет два случая.

1) Проведем \(MO_1\) и \(NO_2\) так, чтобы точки \(M\) и \(N\) лежали по одну сторону от прямой \(O_1O_2\).
Проведем \(NK\) и \(MK\).



Так как \(O_1M\parallel O_2N\), то \(\angle NO_2K=120^\circ\). Следовательно, так как \(\triangle NO_2K\) равнобедренный, то \(\angle O_2KN=30^\circ\).
\(\angle MO_1K=120^\circ\) как смежный с \(\angle MO_1O_2\). Так как \(\triangle MO_1K\) тоже равнобедренный, то \(\angle O_1KM=30^\circ\). Следовательно, прямые \(NK\) и \(MK\) наклонены под углом \(30^\circ\) к прямой \(O_2K\) и имеют общую точку, то есть они совпадают. Это значит, что точка \(M\) лежит на отрезке \(NK\).

Заметим, что \(\triangle TMK\) прямоугольный, следовательно, \[\cos 30^\circ=\dfrac{MK}{TK} \quad\Leftrightarrow\quad \dfrac{\sqrt3}2=\dfrac{MK}{22}\quad\Leftrightarrow\quad MK=11\sqrt3.\] По теореме косинусов из \(\triangle NO_2K\): \[NK=\sqrt{24^2+24^2-2\cdot 24^2\cdot \cos 120^\circ}=24\sqrt3.\] Следовательно, \[NM=NK-MK=13\sqrt3.\]

2) Проведем \(MO_1\) и \(NO_2\) так, чтобы точки \(M\) и \(N\) лежали по разные стороны от прямой \(O_1O_2\).

Продолжим радиус \(MO_1\) за точку \(O_1\) и получим диаметр \(MM'\). Тогда \(M'O_1\parallel O_2N\) и, как в первом случае, точки \(N, M'\) и \(K\) лежат на одной прямой.
Соединим также точки \(M\) и \(K\) и получим прямоугольный \(\triangle MNK\) (\(\angle K=90^\circ\), так как опирается на диаметр \(MM'\)).
Заметим, что \(\triangle NO_2K\) равносторонний, следовательно, \(NK=O_2N=24\).
Рассмотрим прямоугольный \(\triangle MTK\) (\(T\) – вторая точка пересечения меньшей окружности с прямой \(O_1O_2\)). Так как \(\triangle MO_1T\) также равносторонний, то \(\angle MTK=60^\circ\), следовательно, \[\sin\angle MTK=\dfrac{MK}{TK}=\dfrac{MK}{22} \quad\Leftrightarrow\quad MK=11\sqrt3.\] Следовательно, по теореме Пифагора \[MN^2=MK^2+KN^2\quad\Leftrightarrow\quad MN=\sqrt{939}\]

Ответ:

\(13\sqrt3\) или \(\sqrt{939}\)

Данная задача имеет два случая.

1) Проведем отрезки \(AO_1\) и \(BO_2\) так, чтобы точки \(A\) и \(B\) лежали по одну сторону от прямой \(O_1O_2\).

Проведем отрезки \(AC\) и \(BC\).



Заметим, что \(\triangle AO_1C\) равнобедренный с углом \(60^\circ\), следовательно, равносторонний и \(AC=O_1C=11\).
Так как \(O_1A\parallel O_2B\), то \(\angle BO_2O_1=120^\circ\). Так как \(\triangle BO_2C\) равнобедренный, то \(\angle BCO_2=(180^\circ-120^\circ):2=30^\circ\). Следовательно, \(\angle ACB=180^\circ-\angle ACO_1-\angle BCO_2=180^\circ-60^\circ-30^\circ=90^\circ\), то есть \(\triangle ACB\) прямоугольный.
По теореме косинусов из \(\triangle BO_2C\) найдем \(BC=\sqrt{21^2+21^2-2\cdot 21^2\cdot \cos 120^\circ}=21\sqrt3\).

Следовательно, по теореме Пифагора \[AB=\sqrt{AC^2+BC^2}=\sqrt{11^2+21^2\cdot 3}=38.\]

2) Проведем отрезки \(AO_1\) и \(BO_2\) так, чтобы точки \(A\) и \(B\) лежали по разные стороны от прямой \(O_1O_2\).

Заметим, что в этом случае отрезок \(AB\) пройдет через точку \(C\) (точку касания окружностей).
Действительно, так как \(\triangle AO_1C\) равнобедренный и угол при вершине равен \(60^\circ\), то он равносторонний, то есть \(\angle O_1CA=60^\circ\). Следовательно, \(\angle ACO_2=180^\circ-60^\circ=120^\circ\).
Аналогично \(\triangle CO_2B\) равносторонний (\(\angle CO_2B=\angle CO_1A=60^\circ\) как накрест лежащие при \(O_1A\parallel O_2B\) и \(O_1O_2\) секущей) и \(\angle O_2CB=60^\circ\). Следовательно, \(\angle ACO_2+\angle O_2CB=120^\circ+60^\circ=180^\circ\), то есть \(\angle ACB\) развернутый, значит, точки \(A, C, B\) лежат на одной прямой.

Из доказанного следует, что \(AC=AO_1=11\), \(CB=BO_2=21\), следовательно, \(AB=11+21=32\).

Ответ:

38 или 32

Данная задача имеет два случая: когда окружности касаются внутренним образом и когда внешним.

1) Пусть окружности касаются внешним образом.

Заметим, что \(\triangle BO_1A\) равнобедренный (\(BO_1=O_1A\) как радиусы), следовательно, \(\angle BO_1A=180^\circ-2\cdot 15^\circ=150^\circ\). Проведем \(BH\perp O_1A\). Тогда \(\angle BO_1H=30^\circ\). Следовательно, \(BH=\frac12BO_1=\frac32\).
Так как \(BH\) — высота \(\triangle BAO_2\), опущенная к \(AO_2\), то \[S_{BAO_2}=\dfrac12BH\cdot AO_2.\] Заметим, что \(\triangle CO_2A\sim \triangle BO_1A\) по трем углам (\(\angle BAO_1=\angle CAO_2=15^\circ\) как вертикальные, \(\triangle CO_2A\) тоже равнобедренный). Следовательно, если провести \(CK\perp AO_2\), то \(\angle CO_2K=30^\circ\) и \(CK=\frac12CO_2=\frac52\). Тогда \[S_{CO_2A}=\dfrac12CK\cdot AO_2\] Следовательно, \[S_{BCO_2}=S_{BAO_2}+S_{CAO_2}=\dfrac12AO_2\cdot (BH+CK)=\dfrac12\cdot 5\cdot \left(\dfrac32+\dfrac52\right)=10.\]

2) Пусть окружности касаются внутренним образом.

Аналогично \(\triangle BO_1A\sim \triangle CO_2A\) и оба равнобедренные, следовательно, если \(BH\perp AO_2\), то \(BH=\frac12 BO_1=\frac32\), так как \(\angle BO_1A=150^\circ\); а также \(CK=\frac12 CO_2=\frac52\). \[S_{BCO_2}=S_{ACO_2}-S_{ABO_2}=\dfrac12 CK\cdot AO_2-\dfrac12BH\cdot AO_2= \dfrac12AO_2\cdot (CK-BH)=\dfrac12\cdot 5\cdot \left(\dfrac52-\dfrac32\right)=\dfrac52\]

Ответ:

2,5 или 10