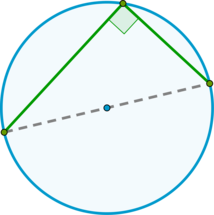
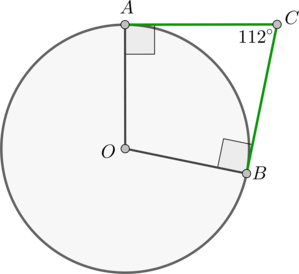
\(AC\) и \(BC\) касаются окружности с центром \(O\). \(\angle OCB = 40^{\circ}\). Найдите \(\angle ACB\). Ответ дайте в градусах.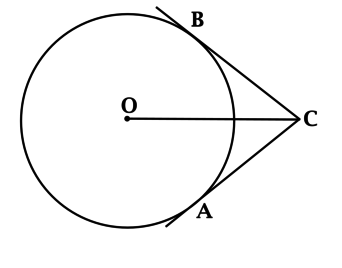
\(OC\) – биссектриса \(\angle ACB\). Покажем это:
Построим радиусы \(OA\) и \(OB\).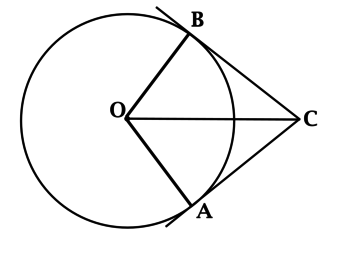
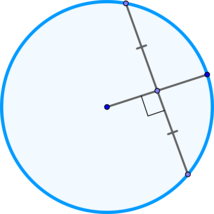
Радиус, проведённый в точку касания, перпендикулярен касательной, следовательно
\(O\) – точка внутри угла \(ACB\), равноудалённая от его сторон. Тогда \(O\) лежит на биссектрисе этого угла (это можно показать через равенство треугольников \(AOC\) и \(BOC\)).
В данной задаче \(\angle OCB = 40^{\circ}\), тогда \(\angle ACB = 2\cdot \angle OCB = 2\cdot 40^{\circ} = 80^{\circ}\).
Ответ: 80