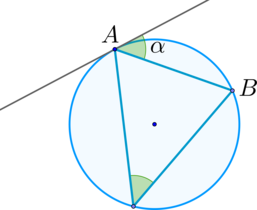
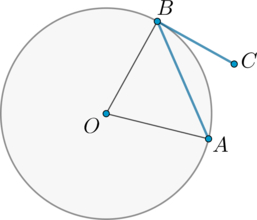
Угол \(ACO\) равен \(24^\circ\). Его сторона \(CA\) касается окружности с центром в точке \(O\). Найдите градусную меру дуги \(AD\), заключенной внутри этого угла, где \(B\) и \(D\) – точки пересечения секущей \(CO\) с окружностью. Ответ дайте в градусах.
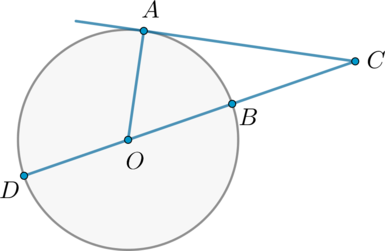
Найдем градусную меру меньшей дуги, стягиваемой хордой \(AB\). Она равна центральному углу \(AOB\), на нее опирающемуся. Так как радиус, проведенный в точку касания, перпендикулярен касательной, то \(\angle OAC=90^\circ\). Следовательно, из \(\triangle OAC\): \(\angle AOC=90^\circ-24^\circ=66^\circ\). Тогда \(\angle AOD=180^\circ-\angle AOC=114^\circ\). Дуга \(AD\), заключенная внутри угла \(ACD\), равна центральному углу \(AOD\) и равна \(114^\circ\).
Ответ: 114